Контрольные вопросы

1.Что такое интегральная схема ?

2.Основные преимущества выполненных на ИС приборов по сравнению с приборами на дискретных схемах.

3.Поясните смысл понятия «микроэлектроеника».

4.Дайте классификацию интегральных схем.

5.Что такое совмещённая ИС ?

6.Как характеризуется функциональная сложность интегральной схемы?

7.Что такое биполярная ИС?

8. Дайте определение МДП ИС.

9.Что такое гибридная ИС?

10. Каким образом в ИС достигается высокая надёжность?

11. Каковы особенности схемотехнических решений в микроэлектронике?

12. Каковы главные направления в развитии микроэлектроники?

13. В чём сущность группового метода производства?

14. Что достигается увеличением размеров кристалла и пластины?

15. В чём заключаются недостатки планарной технологии?

Глава 2. Полупроводники. Полупроводниковые переходы и контакты.

2.1.Свойства полупроводников. В первом приближении к полупроводникам относят вещества с удельным сопротивлением в диапазоне от 10^-3 до 10⁹ Ом·см. В настоящее время для изготовления ИС наиболее широко применяется кремний, заметным конкурентом ему становится арсенид галлия GaAs.

Полупроводники как правило – монокристаллы, то есть твёрдые тела с регулярной структурой. Связь атомов в кристаллической решётке является ковалентной (или просто валентной), а периодичность структуры кристалла приводит к зависимости его свойств от направления в кристаллической решётке – к анизотропии. Кристаллографические плоскости обозначают трёхзначными индексами Миллера, например (111), (100) и т.п. Для разных кристаллографических параметры кристалла: оптические свойства, параметры травления и др. Поэтому пластины для изготовления ИС заранее шлифуют по заданной кристаллографической плоскости.

У атомов на поверхности кристалла часть валентных связей нарушается из-за отсутствия «соседей» по другую сторону границы раздела. Это приводит к нарушению энергетического равновесия на поверхности, которое восстанавливается либо изменением расстояний между атомами, либо путём захвата чужеродных атомов из окружающей среды, либо образованием химических соединений (окислов) на поверхности и т.п. Следовательно, структура тонкого приповерхностного слоя ( несколько нм и менее) отличается от структуры основного объёма кристалла, поэтому и электрофизические параметры приповерхностного слоя заметно отличаются от таковых объёма и этот объём следует рассматривать как особую область кристалла. Эта область играет важную роль в микроэлектронике, поскольку элементы планарных ИС расположены непосредственно под поверхностью, а размеры рабочих областей часто соизмеримы с толщиной граничных слоёв.

Энергетические зонные диаграммы металла, полупроводника и диэлектрика изображены на рис. 2.1. Верхняя разрешённая зона называется свободной или зоной проводимости, а расположенная непосредственно под ней разрешённая зона – валентной зоной. При нулевой заполнена только в нижней части (для металлов), либо полностью пуста (для полупроводников и диэлектриков).

Энергетические диаграммы на рис.2.1 построены для электрона. Когда энергия электрона увеличивается, электрон занимает более высокое положение в зонной диаграмме. Энергия электрона (и дырки) измеряется в электрон-Вольтах(эВ).

Ширина запрещённой зоны равна

φ_з = φ_с - φ_υ,

где φ_с и φ_υ – соответственно энергетические уровни для дна зоны проводимости и потолка валентной зоны.

Ширина запрещённой зоны зависит от температуры

φ_з = φ_з0 – ε_зТ,

где φ_з0 – ширина зоны при Т = 0,

Т – абсолютная температура,

ε_з – температурная чувствительность.

Для кремния ε_з = 3·10^-4 В/ºС, а при комнатной температуре

φ_з = ~1,11 В.

а б в

а – металл; б – диэлектрик; в – полупроводник.

I – зона проводимости; II – валентная зона; III – запрещённая зона.

Рис. 2.1

Энергию, соответствующую середине зоны, называют электростатическим потенциалом проводника

φ_Е = 0,5(φ_с + φ_υ).

В полупроводнике одновременно присутствуют электроны и дырки, порождённые двумя причинами: 1) возбуждением собственного полупроводника n_i и p_i; 2) возбуждением донорных и (или) акцепторных примесей. При этом полные концентрации носителей заряда для примесного полупроводника будут n = n_n + n_i и p = p_i (для донорного); p = p_n + p_i и n = n_i (для акцепторного); при полной ионизации примесей n_n = N_D – количеству доноров, а p_p = N_A – количеству акцепторов. Обычно вследствие малой энергии возбуждения примесей эти величины значительно выше собственных концентраций, то есть n_n >> n_i и p_n>> p_i, поэтому концентрации основных носителей определяются выражениями n = N_D (на самом деле n = N_D – N_A, но N_D >> N_A) для донорного полупроводника и p = N_A для акцепторного полупроводника.

2.2.Распределение носителей в зонах проводимости. В разрешённых зонах находится огромное число уровней, на каждом из которых могут находиться электроны (10²² – 10²³ в 1 см³). Фактическое же количество электронов определяется концентрацией доноров и температурой. Для оценки фактической концентрации носителей нужно знать распределение уровней и вероятность их заполнения.

Энергетическое распределение электронов в твердом теле как частиц, относящихся к фермионам, определяется статистикой Ферми-Дирака. Функция распределения Ферми-Дирака определяет вероятность того, что электрон занимает уровень, соответствующий потенциалу φ:

,

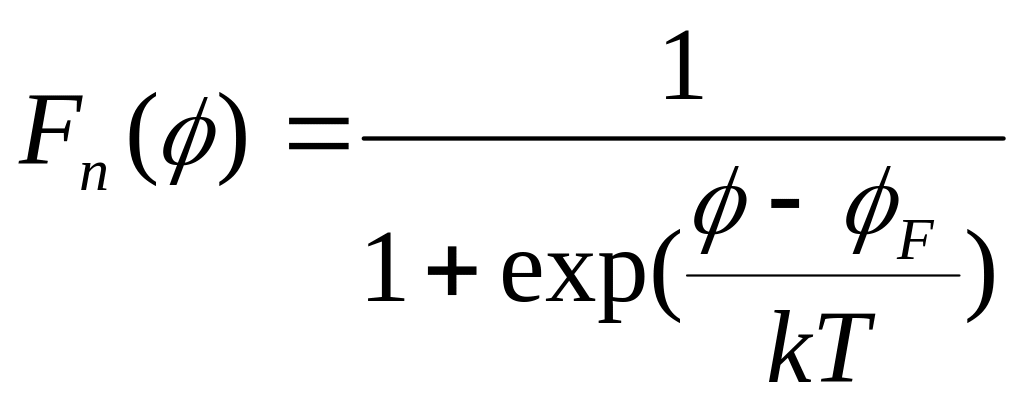где kT – температурный потенциал, Т – абсолютная температура, k – постоянная Больцмана, φ_F – уровень Ферми.

Уровень Ферми можно определить как потенциал, для которого вероятность заполнения точно равна одной второй. Для собственного полупроводника уровень Ферми находится посередине запрещённой зоны, для полупроводника n-типа концентрация электронов больше в зоне проводимости в сравнении с собственным, а для полупроводника р-типа –меньше. Это различие графически отображено на рис. 2.2.

Для потенциалов φ таких, что экспонента в формуле Ферми-Дирака становится значительно больше единицы, можно эту формулу заменить распределением Максвелла-Больцмана

F_n(φ )= exp(- .

а – собственный полупроводник; б – полупроводник n-типа; в – полупроводник р-типа.

Рис. 2.2

Определено, что полная концентрация свободных электронов n в зоне проводимости определяется так:

.

Здесь N_c – так называемая эффективная плотность уровней (состояний) в зоне проводимости:

N_c = 0,5 · 10¹⁶ (m_n/m)^3/2 Т^3/2,

где m_n – эффективная масса электрона.

Для концентрации дырок справедливо

p = .

Здесь N_υ – эффективная плотность уровней (состояний) в валентной зоне:

N_υ = 0,5 · 10¹⁶ (m_p/m)^3/2 Т^3/2,

где m_p – эффективная масса дырки. Для кремния N_c/N_υ = 2,8. Для простоты часто полагают N_c = N_υ.

Произведение концентраций электронов и дырок легко представить в следующем виде:

.

Как видим, при постоянной температуре произведение концентраций есть величина постоянная, так что увеличение одной из концентраций сопровождается уменьшением другой.

В собственном полупроводнике n = p = n_i, поэтому из последней формулы можно получить:

_.

Отметим полную зависимость n_i от ширины запрещённой зоны и температуры.

Полагая N_c = N_υ и учитывая, что φ_E = 0,5(φ_c +φ_υ), нетрудно получить следующее отношение:

.

Учитывая, что p = n_i²/n, можно определить уровень Ферми таким образом:

φ_F = φ_E + φ_T·ln(n/n_i).

Если взять n = n_i²/p, то получим

φ_F = φ_E - φ_T·ln(р/n_i).

Слагаемые φ_T·ln(n/n_i) и φ_T·ln(n/n_i) называются химическим потенциалом. Следовательно, уровень Ферми есть сумма электрического и химического потенциалов. Отсюда ещё одно его название – электрохимический потенциал.

Уровень Ферми одинаков во всех частях равновесной системы, какой бы разнородной она ни была.

Это положение можно записать в виде двух равных по смыслу выражениях:

φ_F = const; grad(φ_F) = 0.

Если концентрация электронов изменяется вдоль координаты х (одномерный случай), то возникает электрическое поле

.

Движение носителей в электрическом поле называют дрейфом. Плотность дрейфового тока определяется известным выражением

j = σЕ,

где σ – удельная проводимость.

Для полупроводника

σ = qnμ_{n +} qpμ_p,

где μ_n и μ_p – подвижности соответствующих носителей.

Для оценки удельной проводимости необходимо знать концентрации электронов и дырок. Руководствуясь условием нейтральности ( n = N_d^*+ p), находим концентрацию электронов в виде:

где N_d^* – концентрация положительных донорных ионов.

Аналогично для концентрации дырок в дырочном полупроводнике:

В рабочем диапазоне температур формулы для концентраций можно упростить по двум причинам.

Во-первых, можно пренебречь концентрацией n_i из-за её малости в сравнении с концентрацией примеси. Во-вторых, эффективную концентрацию примесных ионов N^* можно заменить концентрацией примесных атомов N, поскольку почти все атомы примеси ионизированы. Тогда концентрации основных носителей запишутся в виде:

n_n = N_d , p_p = N_a.

Критическую температуру Т_кр можно определить по формуле

,

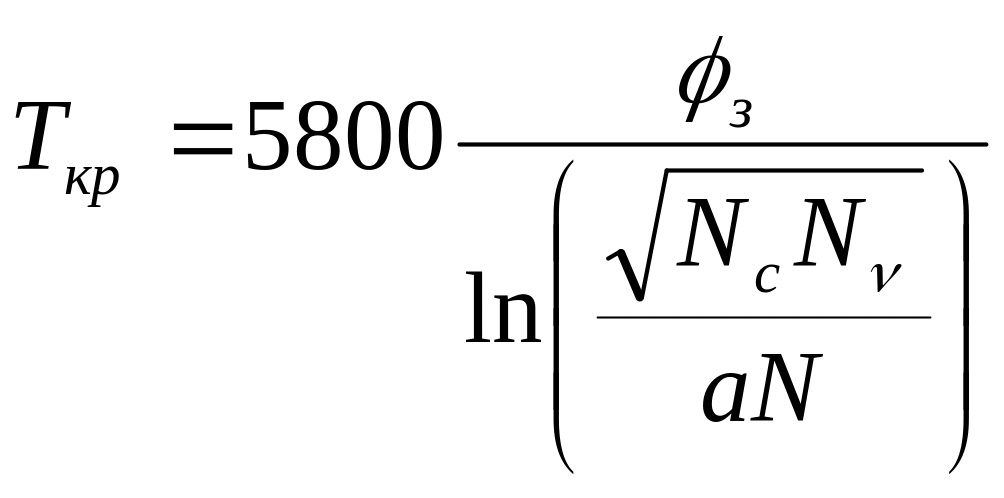где N – концентрация примеси, а N_c и N_υ зависят от температуры.

В свободном пространстве под действием электрического поля электроны совершают равноускоренное движение. В твёрдом теле движущиеся электроны непрерывно сталкиваются с узлами кристаллической решётки, примесями и дефектами – испытывают рассеяние, Равноускоренное движение возможно только в промежутках между столкновениями, на длине свободного пробега. В результате средняя дрейфовая скорость носителей оказывается вполне определённой величиной, пропорциональной напряжённости поля:

υ_ср = μЕ.

Коэффициент пропорциональности μ есть подвижность носителей, измеряемая в единицах см²/В·с. Как правило, подвижность электронов больше подвижности дырок (у кремния почти в три раза).

Подвижность зависит наиболее заметно от температуры, концентрации примесей и напряжённости поля. Если рассеяние преобладает на узлах решётки, то

μ_L = μ_0L(T₀/T)^c,

если же преобладает рассеяние на ионах примеси, то

μ_I = μ_0I(T/Т₀)^3/2.

Значения μ₀ относятся к исходной температуре Т₀, а значения μ – к температуре Т (Кельвина). Показатель степени с зависит от материала и типа проводимости. Для кремния электронного и дырочного с ≈ 5/2.

Применительно к собственному полупроводнику, для которого n = p = n_i, выражение удельной проводимости принимает вид

σ_i = qn_i(μ_n + μ_p).

Для примесных полупроводников (электронного и дырочного) получаем, при пренебрежении составляющими, связанными с неосновными носителями

σ_n = qN_Dμ_n;

σ_p = qN_Aμ_p;

В рабочем диапазоне температуры концентрации N_D и N_A можно считать постоянными и поэтому в этом диапазоне температурная зависимость проводимости примесного полупроводника определяется температурной зависимостью подвижности.

В рабочем диапазоне зависимость σ(Т) для примесных полупроводников несравненно слабее, чем для собственного.

2.3. Эффект поля. Эффектом поля называют изменение концентрации носителей (а, значит и проводимости) в приповерхностном слое полупроводника под действием электрического поля. Слой с повышенной по сравнению с объёмом концентрацией основных носителей называют обогащённым, а слой с пониженной их концентрацией – обеднённым.

На рис.2.3 между металлической пластинкой и полупроводником, разделённых диэлектриком, приложено напряжение U. В такой системе МДП тока нет, поэтому она равновесна и по сути является конденсатором, одна из обкладок которого есть полупроводник. На этой обкладке наведён такой же заряд, как и на металлической. Но заряд в полупроводнике не сосредоточен на поверхности, а распространяется на некоторое расстояние в глубь кристалла.

Электрическое поле распределяется между диэлектриком и полупроводником. Поле в диэлектрике Е_d постоянное (нет объёмных зарядов), а в полупроводнике – непостоянное, так как заряд спадает от поверхности в глубь полупроводника.

При отрицательной полярности металла (рис. 2.3) наведённый заряд положителен. В р-полупроводнике положительный заряд обусловлен дырками, притянувшимися к поверхности (обогащение слоя), а в n-полупроводнике – ионами доноров, от которых оттолкнулись электроны (обеднение слоя основными носителями).

Протяжённость подвижных зарядов в обогащённом слое называют длиной Дебая, а протяжённость неподвижных ионных зарядов – глубиной обеднённого слоя.

Рис. 2.3.

Из-за наличия зарядов между объёмом и поверхностью между ними возникает разность потенциалов, называемая поверхностным потенциалом,φ_s.

При отсутствии внешнего напряжения значение φ_s имеет конечную равновесную величину φ_s0. Внешнее напряжение, компенсирующее потенциал φ_s0, называется напряжением спрямления зон и обозначается U_F.

Расстояние d не может быть произвольно малым; при d<10нм диэлектрик становится проницаемым для подвижных носителей благодаря туннельному эффекту. При этом структура МДП перестаёт быть аналогом конденсатора.

В общем случае плотность заряда в полупроводнике записывается следующим образом:

λ = q(p + N_D^* – n – N_A^*).

Концентрации свободных носителей связаны с величиной электростатического потенциала φ_Е так:

,

где n₀ и р₀ – концентрации электронов и дырок в глубине полупроводника, где заряды и поле отсутствуют.

Для собственного полупроводника полагаем n₀ = p₀ = n_i и N_D* = N_A^* = 0. Тогда плотность заряда приводится к виду

λ = -2qn_ish(φ/kT).

Дебаевская длина в этом случае определяется выражением:

.

Для кремния l_Di ≈ 14 мкм. Дебаевская длина – это расстояние, на котором потенциал уменьшается в ℮ раз по сравнению с максимальным значением φ_s на поверхности.

Распределение потенциала в области объёмного заряда определятся следующей функцией:

φ(x) ≈ φ_s exp(-x/l_Di).

Графически эта функция представлена на рис. 2.4. Искривление энергетических зон вблизи границы диэлектрик – полупроводник есть характерная особенность эффекта поля. Если изменить полярность напряжения, то знак объёмного заряда изменится, и зоны искривятся в другую сторону – «вниз». Однако при обеих полярностях

Рис. 2.4

приповерхностный слой в собственном полупроводнике оказывается обогащённым либо электронами, либо дырками. Отметим, что поверхностный потенциал составляет тем большую долю приложенного напряжения, чем тоньше диэлектрик. При всех реальных значениях толщины диэлектрика и приложенного напряжения поверхностный потенциал не превышает нескольких десятых долей Вольта.

В примесных полупроводниках возможно получение как обогащённых, так и обеднённых слоёв

Режим обогащения соответствует такой полярности приложенного напряжения, при которой основные носители притягиваются к поверхности. Этот случай близок к рассмотренному на рис. 2.4, но отличается меньшим искривлением зон: примесный полупроводник богат подвижными носителями и поэтому даже небольшой поверхностный потенциал обеспечивает необходимый заряд вблизи поверхности.

При условии φ_s < 2kT дебаевская длина имеет вид:

,

где N – концентрация ионизированной примеси (донорной или акцепторной).

Так как N >> n_i , дебаевская длина в примесных полупроводниках значительно меньше, чем в собственных. Типичное значение l_D ≈ 0,04 мкм, то есть поле проникает в примесные полупроводники на ничтожную глубину.

Режим обеднения соответствует такой полярности приложенного напряжения, при которой основные носители отталкиваются от поверхности. В этом случае поверхностный потенциал может иметь гораздо большие значения, чем в режиме обогащения. Отталкивание основных носителей приводит к появлению некомпенсированного объёмного заряда примесных ионов.

Протяжённость (толщина) обеднённого слоя определяется из соотношения:

.

Обычно величина l₀ в несколько раз превышает величину l_D.

С ростом напряжения основные носители продолжают отталкиваться (а обеднённый слой расширяться), но одновременно к поверхности притягиваются неосновные носители. Когда заряд неосновных носителей превысит заряд оставшихся основных, изменится тип проводимости слоя около поверхности. Этот случай характеризуют термином инверсия типа проводимости, а образованный неосновными носителями слой называют инверсионным слоем (рис. 2.5).

Рис. 2.5

С точки зрения зонной теории образование инверсионного слоя объясняется тем, что вблизи поверхности уровень электростатического потенциала пересекает уровень Ферми, так что на приповерхностном участке уровень Ферми оказывается в той половине запрещённой зоны, которая соответствует преобладанию неосновных носителей. Толщина инверсионного слоя составляет всего 1-2 нм, то есть 3-4 постоянных решётки.

2.4. Законы движения носителей в полупроводниках. В общем случае движение носителей заряда обусловлено двумя процессами: диффузией под действием градиента концентрации и дрейфом под действием градиента электрического потенциала. Естественно, что полный ток состоит из четырёх составляющих:

j = (j_n)_др + (jn)_дф +(j_p)_др + (j_p)_дф.

В формуле указаны плотности токов (удобнее при анализе). В одномерном случае

(j_n)_др =qnμ_nE = -qnμ_n(∂φ/∂x);

(j_p)_др =qnμ_pE = -qnμ_p(∂φ/∂x);

Диффузионные составляющие

(j_n)_дф = qμ_nkT·dn/dx = qD_n·dn/dx;

(j_p)_дф = -qμ_pkT·dp/dx = qD_p·dp/dx.

Коэффициенты D_n и D_p называются коэффициентами диффузии электронов и дырок.

Формула Эйнштейна:

D = kTμ.

Дрейфовые составляющие пропорциональны n и p (концентрациям), а диффузионные определяются только градиентами концентраций.

В общем случае концентрации зависят от координат и времени, то есть n = n(x,t) и p = p(x,t). Эти функции есть решения уравнений непрерывности потока:

dn/dt = Δg – (n –n₀)/τ + (1/q)·div(j_n);

dp/dt = Δg – (p –p₀)/τ + (1/q)·div(j_p),

где n – n0 = Δn и p – p0 = Δp – избыточные концентрации, Δg – скорость генерации носителей под действием внешних факторов (света и др.); τ – время жизни избыточных носителей.

В одномерном случае

div(j/q) = (1/q)·∂j/∂x.

Используя эту операцию и опуская Δg , запишем уравнения непрерывности так:

∂n/∂t = -(n – n0)/τ + D_n·∂²n/∂x² +μ_nE(∂n/∂x) +nμ_n(∂E/∂x);

∂n/∂t = -(p – p0)/τ + D_p·∂²p/∂x² - μ_nE(∂p/∂x) - nμ_n(∂E/∂x);

последние слагаемые связаны с наличием объёмных зарядов.

При отсутствии поля Е = 0. Тогда

∂n/∂t = -(n – n0)/τ + D_n·∂²n/∂x² ;

∂n/∂t = -(p – p0)/τ + D_p·∂²p/∂x² .

Последние уравнения – уравнения диффузии.

При падении на поверхность полупроводника пучка света (рис. 2.6) в тонком приповерхностном слое рождаются электронно-дырочные пары. Между поверхностью и объёмом возникнут градиенты концентрации и как следствие – дрейф избыточных носителей вглубь полупроводника. Такое движение носителей называют биполярной или амбиполярной диффузией. Из-за более высокой подвижности электроны несколько обгоняют поток дырок, возникает небольшой объёмный заряд и соответствующее электрическое поле, которое тормозит поток электронов и ускоряет дырки. Устанавливается стационарный режим в виде двух сдвинутых относительно друг друга «облачков» (электронов и дырок), которые движутся синхронно, так что суммарный ток отсутствует. Описанное явление есть эффект Дембера с демберовским полем и демберовским напряжением

При монополярной диффузии в приповерхностный слой вводятся только неосновные носители – инжекция. Уровнем инжекции называют отношение концентрации избыточных носителей к равновесной концентрации основных носителей (концентрации примесей):

δ = Δn/N.

Если интерес представляют только избыточные концентрации, достаточно использовать одно из двух

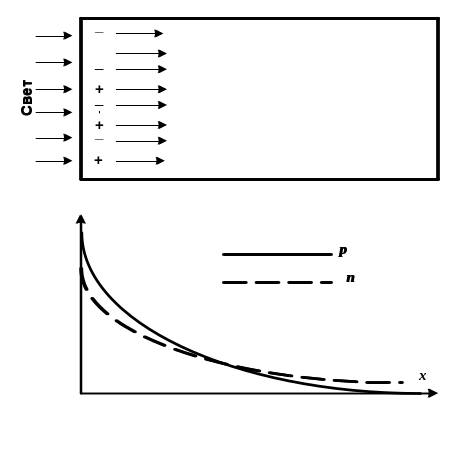
Рис. 2.6

.

уравнений диффузии, которое принимает вид:

∂²(Δn)/∂x² – Δn/L² = (1/D)∂(Δn)/∂t.

Стационарный вариант уравнения получается при ∂(Δn)/∂t = 0.

Величина есть средняя диффузионная длина и характеризует среднее расстояние, на которое носители могут продиффундировать за время жизни. Для кремния значения L cоставляют 5 – 20 мкм в зависимости от времени жизни.

Решение стационарного уравнения диффузии имеет вид:

Δn(x) = Δn(0)exp(-x/L).

Следовательно, на расстоянии диффузионной длины избыточная концентрация уменьшается в ℮ раз. На участке длиной (3-4)L концентрация уменьшается в 20-50 раз, то есть становится пренебрежимо малой по сравнению с граничной концентрацией.

Дифференцируя последнее уравнение, получаем градиент концентрации

d(Δn)/dx = - [Δn(0)/L] exp(-x/L).

Как видно, градиент концентрации (значит, и диффузионный ток) спадает при удалении от поверхности вглубь кристалла и имеет максимальное по модулю значение при x = 0, то есть на инжектирующей поверхности:

d(Δn)/dx | _x=0 = - [Δn(0)/L].

2.5. Электронно-дырочные переходы. Комбинация двух полупроводниковых слоёв с разным типом проводимости обладает вентильными свойствами, то есть гораздо лучше пропускает ток в одном направлении (рис. 2.7). Прямое напряжение соответствует большему току (прямому току), а обратное напряжение – меньшему току (обратному току).

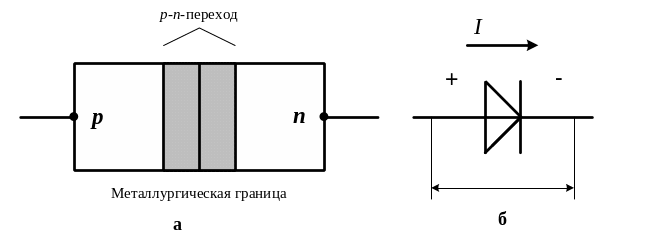Рис. 2.7

Вентильные свойства структуры позволяют применять её

в качестве полупроводникового диода (рис. 2.7,б).

Поверхность контакта р и n слоёв называется металлургической границей, прилегающая к ней область объёмных зарядов – р-n- переходом. Внешние контакты в диоде – невыпрямляющие (омические).

Ступенчатые переходы имеют идеальную границу, по одну сторону которой – доноры с постоянной концентрацией N_D , а по другую – акцепторы с постоянной концентрацией Na.

Плавные переходы имеют в районе металлургической границы постепенное уменьшение концентрации одного типа и увеличение другого. Граница в этом случае соответствует равенству N_D = Na.

Симметричные переходы характеризуются условием N_Dn ≈ Nap, они не типичны для полупроводниковой техники.

При резкой асимметрии (различие концентраций на 1-2 порядка и более) переходы называют односторонними и обозначают n⁺-p или p⁺-n.

На рис. 2.8 показана электрическая структура р-n-перехода. Для наглядности разница в концентрациях основных носителей принята меньшей, чем это имеет место в действительности.

Рис. 2.8

В большинстве случаев р-n-переход можно идеализировать так, как показано на рис. 2.8,в, то есть совсем пренебречь наличием свободных носителей в переходе и считать границы перехода идеально резкими. Такая идеализация упрощает решение многих задач.

Переход в целом нейтрален, однако плотности зарядов резко различны: в слое с меньшей концентрацией примеси ( в нашем случае в р-слое) область объёмного заряда много шире. Говорят, несимметричный переход сосредоточен в высокоомном слое. Следует обратить внимание на факт, что внутри перехода есть участок с собственной (значит – минимальной) концентрацией носителей. Поэтому область перехода – наиболее высокоомная часть всей диодной структуры.

На рис. 2.9 представлены зонные диаграммы p-n перехода до и после соприкосновения слоёв. Единство уровня Ферми в равновесном переходе приводит к искривлению зон в области металлургической границы и образованию разности потенциалов (потенциальный барьер) и электрического поля. Высота потенциального барьера определяется так:

Δφ₀ = φ_Ep – φ_En.

Рис. 2.9

Для равновесного состояния справедливо

Δφ₀ = kT ln(n_n0 p_p0 /n_i²).

Если положить n_n0 = N_d и p_p0 = N_a (N_d и N_a – эффективные концентрации примесей), то

Δφ₀ = kT ln(N_dN_a /n_i²).

При прочих равных условиях высота потенциального барьера тем выше, чем меньше собственная концентрация. Для кремния при N_d = 10¹⁹ cм^-3 , N_a = 10¹⁶ см^-3 и n_i = 2·10¹⁰ см^-3 получаем для комнатной температуры Δφ₀ = 33kT ≈ 0,83 В.

Концентрации основных носителей можно заменить на концентрации неосновных, что позволяет записать

Δφ₀ = kT ln(n_n0 /n_p0).

Δφ₀ = kT ln(p_p0 /p_n0).

Следовательно, равновесная высота потенциального барьера определяется отношением концентраций однотипных носителей по обе стороны перехода, на его границах.

Решение уравнения Пуассона позволяет получить соотношение между составляющими ширины перехода в р- и n-слоях :

ℓ_n/ℓ_p = N_a/N_d.

Из решения этого же уравнения можно определить высоту потенциального барьера как функцию концентраций и составляющих ширины перехода:

Δφ₀ = .

Для несимметричных переходов одним из слагаемых можно пренебречь, что приводит к следующей формуле ширины потенциального барьера:

,

где N – концентрация примеси в высокоомном слое перехода. Полагая Δφ₀ = 0,8 В и N = 10¹⁶ cм^-3, получаем для кремния l₀ ≈ 0,3 мкм.

Для плавных переходов, считая плотности объёмных зарядов линейными функциями координаты, можно получить ширину равновесного перехода в виде:

,

где N′ – градиент эффективной концентрации.

Так как градиент одинаков в обеих частях перехода, то ширина его делится поровну между р- и n- слоями. Плавный переход симметричен.

При подключении источника э.д.с. U между р- и n- слоями равновесие перехода нарушится и в цепи потечёт ток. Внешнее напряжение почти полностью падает на переходе, поэтому, когда э.д.с. U приложена плюсом к р-слою, высота барьера уменьшается

Δφ = Δφ₀ – U.

Напряжение такой полярности является прямым. При минусе на р-слое высота барьера увеличивается

Δφ = Δφ₀ + U.

С высотой барьера меняются его ширина и граничные концентрации носителей. Для неравновесного барьера имеем

Как видно, переход сужается при прямом напряжении (U > 0) и расширяется при обратном (U < 0).

Связь между граничными концентрациями неосновных носителей в равновесном и неравновесном состояниях такова:

Δn_p = n_p0(℮^U/kT – 1);

Δp_n = p_n0(℮^U/kT – 1);

Δn_p/Δp_n = N_D/N_A.

Следовательно, у несимметричных переходов концентрация избыточных носителей в высокоомном слое много больше, чем в низкоомном. Инжектирующий слой называют эммитером, а слой, в который направлена инжекция, – базой.

2.6. Вольт-амперная характеристика р-n перехода. В общем случае ток перехода состоит из электронной и дырочной составляющих, каждая из которых содержит инжекционную и рекомбинационную компоненты. При выводе идеализированной вольт-амперной характеристики (ВАХ) рекомбинационной компонентой пренебрегают.

Принимая, что токи инжектированных носителей чисто диффузионные, можно получить электронную и дырочную части тока в виде:

С физической точки зрения токи протекают от «плюса» к «минусу», то есть являются положительными. Суммируя части тока, умножая их сумму на площадь перехода S и опуская знак минус, запишем ВАХ перехода

где

.

Формула для ВАХ – одна из важнейших в транзисторной теориии. Её начальный участок представлен на рис. 2.10 в относительных единицах. Эта ВАХ – идеальная, но именно ею пользуются при анализе и расчёте полупроводниковых приборов в электронике.

Ток I₀ называется тепловым и сильно зависит от температуры. Из формулы для ВАХ следует, что при |U| > 3kT и U отрицательном величина обратного тока равна –I₀ и не зависит от U.

В несимметричных переходах составляющие теплового тока существенно различаются. Для n⁺-p-перехода главной является электронная составляющая, которую можно записать таким образом

I₀ = (qDS/LN)n_i²

Если N = 10¹⁶см^-3 и L = 10мкм, то при Т ≈ 300 К j₀ ≈ 2·10^-10А/см². У современных интегральных транзисторов

Рис. 2.10

площади баз не превышают 2·10^-5см², а площади эммитеров – 10^-6см², так что типичным значением теплового тока при Т = 300К можно считать I₀ = 10^-15A.

Температурная зависимость тока I₀ определяется так

I₀ = I₀₀·exp(ф_з/kT).

При U>0 зависимость I(U) чрезвычайно крута, поэтому для р-n-переходов характерен режим заданного тока. ВАХ можно записать в такой форме:

.

При ничтожном значении I₀ справедливо

U = kT·ln(I/I₀)

На практике диапазон изменения тока I невелик, поэтому и прямое напряжение меняется незначительно. В зависимости от диапазона токов прямые напряжения несколько различаются, но в пределах диапазона их можно считать постоянными и рассматривать как своего рода параметр открытого перехода.

Один из важнейших параметров прямой ветви ВАХ есть дифференциальное сопротивление перехода:

r_p-n = dU/dI = kT/I.

Заменим дифференциалы конечными приращениями

ΔU = ΔI•r_p-n.

Значит, r_p-n есть сопротивление для приращений тока ΔI, малых по сравнению с постоянной составляющей тока I. Типичным значением является r_p-n = 25 Ом при I = 1мА.

Реальный обратный ток перехода намного превышает теоретическую величину I₀ из-за генерации n-p пар в области обратно смещённого перехода. Обусловленную этим явлением компоненту обратного тока называют током термогенерации. При больших обратных напряжениях возможны три типа пробоя p-n перехода: туннельный, лавинный и тепловой.

Туннельный пробой объясняется квантово-механическим преодолением электронами тонкого потенциального барьера. В основе лавинного пробоя – «размножение» носителей в сильном электрическом поле в области перехода. Тепловой пробой обусловлен саморазогревом перехода при протекании обратного тока.

Диод обладает емкостью, которую можно считать подключённой параллельно p-n переходу. Эту ёмкость разделяют на две составляющие: барьерную, отражающую перераспределение зарядов в переходе, и диффузионную, отражающую перераспределение в базе. Обе ёмкости нелинейны. Заслуживает рассмотрения барьерная ёмкость, которая является удобным параметром. В транзисторной электронике часто пользуются дифференциальной барьерной ёмкостью (на единицу площади):

В формуле Δφ₀ – равновесная высота барьера, U – обратное напряжение (имеет отрицательный знак).

2.7.Контакты полупроводник-металл (MS). В ИС контакты металл-полупроводник применяются как невыпрямляющие (соединения элементов в ИС) и как специфические выпрямляющие (диоды Шоттки). Структура и свойства контактов MS зависят от взаимного расположения уровней Ферми. На рис. 2.11 вверху – зонные диаграммы раздельных слоёв, а внизу – зонные диаграммы контактов. На рис. 2.11,а φ_Fm > φ_Fp, поэтому часть электронов из металла перейдёт в полупроводник р-типа. Из-за рекомбинации вблизи границы с металлом «обнажаются» некомпенсированные отрицательные ионы акцепторов. Появляется электрическое поле, энергетические уровни искривляются вниз. На рис. 2.11,б – противоположный случай. Область искривления зон (область объёмных зарядов) в обоих случаях имеет протяжённость порядка 0,1-0,2 мкм. Контакты такого рода создаются напылением металла на полупроводник.

Обмен электронами между металлом и полупроводником обычно характеризуют разностью работ выхода φ_MS = φ_M- φ_S, которую называют контактной разностью потенциалов.

При φ_М < φ_S электроны переходят из металла в полупроводник (рис.2.11,а), а при φ_М > φ_S – из полупроводника в металл (рис. 2.11,б).

Потенциальный барьер в приконтактном слое называют барьером Шоттки. Контакты, показанные на рис. 2.11, обладают выпрямляющими свойствами и могут быть основой диодов (диодов Шоттки).

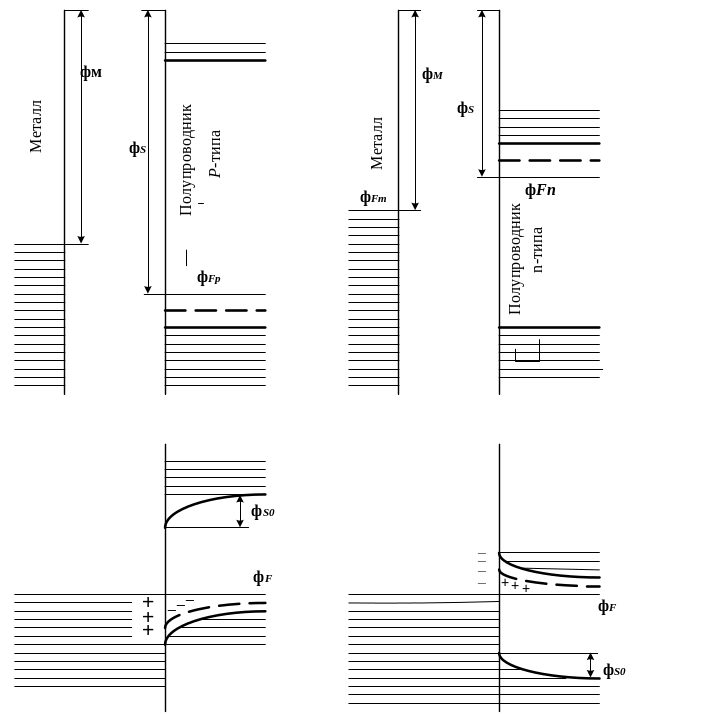
а б

Рис. 2.11

Важнейшая особенность диодов Шоттки – отсутствие инжекции неосновных носителей (работают на основных носителях). Поэтому у диодов Шоттки нет диффузионной ёмкости, что существенно повышает быстродействие диодов при изменениях токов и напряжений, в том числе с прямых на обратные и наоборот, до десятых и сотых долей нс.

Кроме того, у диодов Шоттки прямое напряжение примерно на 0,2 В меньше, чем у р-n –перехода, и имеет типичное значение 0,4 В. У этих же диодов прямая ветвь ВАХ строго подчиняется экспоненциальному закону в широком диапазоне токов (от 10 до 10 А), что позволяет использовать такие диоды как прецизионные логарифмирующие элементы.

Барьеры Шоттки образуются в кремнии при контакте с такими металлами, как молибден, нихром, золото, платина и алюминий.

Если при контакте металла с полупроводником р-типа имеет место неравенство φ_МS > 0, а при контакте с полупроводником n-типа φ_МS < 0, то в первом случае электроны будут переходить из полупроводника в металл (зоны искривятся «вверх»), а во втором случае – из металла в полупроводник (зоны искривятся «вверх»). В таких контактах вблизи границы в полупроводнике накапливаются основные носители – образуются обогащённые слои с протяжённостью сотых долей мкм. При φ_МS > 0,1(0,2) В уровень Ферми пройдёт через соответствующую разрешённую зону и полупроводник превращается в полуметалл с очень малым удельным сопротивлением. Такие невыпрямляющие контакты называются омическими.

2.8.Граница полупроводник – диэлектрик. Здесь мы рассмотрим структуру Si-SiO₂. Особенность плёнок SiO₂ состоит в том, что они всегда содержат примеси донорного типа – натрий, калий и водород, сосредоточенные вблизи границы с кремнирем. Отданные донорами электроны переходят в приповерхностный слой кремния, создавая типичные приповерхностные концентрации (0,5-2,0)·10^-12см^-2 .

Если у кремния проводимость n-типа, то перешедшие в него из окисла электроны обогащают его приповерхностный слой основными носителями: образуется так называемый

Рис. 2.12

n-канал (рис. 2.12, а). В кремнии с р-типа проводимостью перешедшие в него из окисла электроны либо обедняют приповерхностный слой, «обнажая» отрицательные ионы акцепторов (рис. 2.12,б), либо образуют вместе с обеднённым слоем тонкий инверсионный слой n-типа (рис. 2.12,в).

Возникновение дополнительных каналов проводимости под слоем SiO₂ в приборах с использованием р-n переходов и МДП может нарушить структуру этих приборов и нормальную работу элементов ИС.