88. Законы распределения: биноминальный, Пуассона, равномерный, показательный, нормальный.

Биномиальный закон (распределение Бернулли)

Производящая функция биномиального распределения задаётся формулой

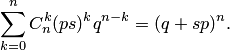
Закон распределения Пуассона (закон редких событий)

Случайная величина   называется распределённой по закону Пуассона с параметром  , если

Производящая функции распределения Пуассона задаётся формулой

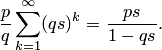
Равномерное распределение задаётся следующим законом:

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Случайная величина   имеет экспоненциальное распределение с параметром  , если её плотность имеет вид

.

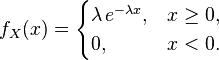Нормальное распределение,^[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:

89. Числовые характеристики дискретных и непрерывных случайных величин.

См. вопрос 87.

90. Статистическое распределение выборки. Полигон и гистограмма.

Полигоном частот называют ломаную, отрезки, которой соединяют точки (х₁,n₁),(х₂,n₂),...,(х_k,n_k). Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты n_i. Точки (х_i,n_i) соединяют отрезками и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х₁,w₁),(х₂,w₂),...,(х_k,w_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты х_i, а на оси ординат соответствующие им частоты w_i. Точки (х_i,w_i) соединяют отрезками и получают полигон относительных частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h. Площадь i-го частичного прямоугольника равна h•n_i/h=n_i - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению w_i/h (плотность относительной частоты).