
- •Определители, их свойства. Миноры и алгебраические дополнения. Различные способы вычисления определителей.
- •Матрицы, основные определения, действия над матрицами.
- •Решение систем линейных алгебраических уравнений методом Гаусса, по правилу Крамера, с помощью обратной матрицы.
- •Векторы, основные определения, понятия, действия над ними.
- •Скалярное произведение ненулевых векторов и равно произведению длины вектора на алгебраическое значение длины ортогональной проекции вектора на ось, задаваемую вектором :
- •Векторное поле, векторные линии. Дивергенция векторного поля.
- •Законы распределения: биноминальный, Пуассона, равномерный, показательный, нормальный.
Векторное поле, векторные линии. Дивергенция векторного поля.
Если каждой точке M заданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое число u, то говорят, что в этой области задано скалярное поле. Скалярное поле – это функция, отображающая R в степени n в R.
Векторные линии (интегральная кривая) для поля F(r) называется кривая r=r(t), касательная к которой во всех точках кривой совпадает со значением поля: dr/dt = F(r(t)).
Дивергенция – дифференциальный оператор, отображающий векторное поле на скалярное ( то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле) который определяет (для каждой точки) насколько расходится входящее и исходящее из малой окрестности данной точки поле. Более краткое определение дивергенции: это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля.
Циркуляция и ротор векторного поля.
Циркуляцией векторного поля по данному замкнутому контуру Г называется криволинейный интеграл второго рода, взятый по Г. По определению C = интеграл по замкнутому контуру Г Fdl = интеграл по замкнутому контуру Fxdx + Fydy + Fzdz
Ротор или вихрь – векторный дифференциальный оператор над векторным полем.
Потенциальные и соленоидальные поля.
Потенциальное (безвихревое) поле – векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трехмерном пространстве является равенство нулю ротора поля.
Векторное поле является соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю.
Числовые ряды, основные определения. Сходимость и сумма ряда.
Числовым рядом называется бесконечная последовательность чисел u1, u2…un соединенных знаком сложения.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растет. Если такой предел существует и конечен, то ряд сходится, в противном случае – расходится.
Знакоположительные ряды. Достаточные признаки сходимости.
Знакоположительным называется ряд, если все числа, входящие в ряд положительны, неотрицательны.
Признак Даламбера. Признак сравнения. Радикальный признак Коши. Интегральный признак Коши.
Знакопеременные ряды. Абсолютная и условная сходимость.
Знакочередующимся рядом называется ряд, если его члены попеременно принимают значения противоположных знаков.
Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Признак Лейбница.
Признак Лейбница – теорема об условной сходимости знакочередующихся рядов.
S=Ряд от 1 до бесконечности bi сходится, если выполняются оба условия: 1. Модуль bi+1 меньше модуля bi. 2.Предел при i, стремящимся к бесконечности модуль bi = 0.
Степенные ряды. Теорема Абеля.
Степенной ряд – это формальное алгебраическое выражение вида: F(X) = Ряд от 0 до бесконечности an*X в степени n
Теорема Абеля. Признак Абеля дает достаточные условия сходимости числового ряда. Числовой ряд от 0 до бесконечности anbn сходится, если выполнены следующие условия: 1. Последовательность an монотонна и ограничена. 2. Числовой ряд от нуля до бесконечности bn сходится.
Ряды Тейлора и Маклорена.
Ряд Тейлора – разложение функции в бесконечную сумму степенных функций. Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд: Ряд от 0 до бесконечности, в знаменателе f в степени k умноженная на a / k! * (x-a) в степени k называется рядом Тейлора функции f в точке a. В случае, если a = 0, этот ряд называется рядом Маклорена.
Разложение функций в степенные ряды.
Функция, аналитическая в области D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда f(z) = Сумма от 0 до бесконечности cn (z-z0) в степени n, радиус сходимости R, которого не меньше, чем расстояние от точки z0 до границы области D. Алгоритм вычисления: найти производные от данной функции, вычислить значения производных в точке z0, найти область сходимости полученного ряда.
Комплексные числа. Алгебраическая, тригонометрическая и показательная формы записи, действия над ними.
Комплексные числа – числа вида x+iy, где x и y – вещественные числа, i – мнимая единица.
Тригонометрическая форма записи ф=ф0+2kп
Показательная форма записи z=re в степени iф
Действия над комплексными числами.
Суммой комплексных чисел z1 и z2 называется комплексное число z=(x1+x2,y1+y2)
Произведением комплексных чисел z1 и z2 называется комплексное число z=(x1x2-y1y2,x1y2-x2y1)
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2+z=z1, откуда z=z1-z2=(x1-x2,y1-y2)
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что z2*z=z1. Отсюда z=(x1x2+y1y2/x2^2+y2^2, x2y1-x1y2/x2^2+y2^2)
Комплексная плоскость. Модуль и аргумент комплексного числа. Главное значение аргумента. Геометрический смысл.
Комплексная плоскость – это двумерное вещественное пространство R^2, которое изоморфно полю комплексных чисел C. Каждая точка такого пространства – это упорядоченная пара вида (x,y), где x и y – вещественные числа, и где первый элемент пары соответствует вещественной части, а второй элемент пары соответствует мнимой части комплексного числа z=x+iy x=Re z, y=Im z
Функция комплексного переменного.
Производная функции комплексного переменного. Условия Коши-Римана.
Интегрирование функции комплексного переменного.
Интегральная формула Коши.
Пусть D – область на комплексной плоскости с кусочно-гладкой границей Г = дельта D, функция f(z) – голоморфна в D и z0 – точка внутри области D. Тогда справедлива следующая формула Коши: f(z0) = 1/2пi * интеграл Г f(z)/z-z0 dz. Формула справедлива также, если предполагать, что f(z) голоморфна внутри D, и непрерывна на замыкании, а также если граница D не кусочно-гладкая, а всего лишь спрямляемая.
Изолированные особые точки, их классификация.
Изолированная особая точка – точка, в некоторой проколотой окрестности которой функция f(z) однозначна и аналитична, а в самой точке либо не задана, либо не дифференцируема.
Классификация.
Устранимая особая точка – называется особой точкой функции f(z), голоморфной в некоторой проколотой окрестности этой точки, если существует конечный предел z стремится к z0 f(z) = B, B принадлежит C.
Полюс – называется голоморфной точкой в некоторой проколотой окрестности этой точки, если существует предел z стремится к z0 f(z) = бесконечность.
Существенно особая точка – называется голоморфной точкой в некоторой проколотой окрестности этой точки , если предел z стремится к z0 f(z) – не существует.
Вычеты и формулы для их вычисления.
Пусть ![]() —
изолированная особая точка функции
—
изолированная особая точка функции ![]() .
По определению изолированной особой
точки существует некоторая окрестность
этой точки, в которой
—
аналитическая. Напомним, что для
.
По определению изолированной особой
точки существует некоторая окрестность
этой точки, в которой
—
аналитическая. Напомним, что для ![]() эта
окрестность имеет вид
эта
окрестность имеет вид ![]() ,
а для
,
а для ![]() —
— ![]()
Вычетом
функции
в
изолированной особой точке ![]() называется
интеграл
называется
интеграл 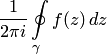 ,
где
,
где ![]() —
контур, принадлежащий окрестности
точки
—
контур, принадлежащий окрестности
точки ![]() и
охватывающий ее.
и
охватывающий ее.
Основная теорема о вычетах
Интеграл по замкнутому контуру f(z)dz = 2пi * Сумма от 1 до n res f(z)
Основы вероятностного анализа.
Классификация событий. Сумма, произведение событий, их свойства, графическое представление.
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Различают события
совместные и несовместные.
События называются совместными, если
наступление одного из них не исключает
наступления другого. В противном случае
события называются несовместными.
Например, подбрасываются две игральные
кости. Событие ![]() —
выпадание трех очков на первой игральной
кости, событие
—
выпадание трех очков на первой игральной
кости, событие ![]() —
выпадание трех очков на второй
кости.
и
—
совместные события. Пусть в магазин
поступила партия обуви одного фасона
и размера, но разного цвета. Событие
—
наудачу взятая коробка окажется с обувью
черного цвета, событие
—
коробка окажется с обувью коричневого
цвета,
и
—
несовместные события.
—
выпадание трех очков на второй
кости.
и
—
совместные события. Пусть в магазин
поступила партия обуви одного фасона
и размера, но разного цвета. Событие
—
наудачу взятая коробка окажется с обувью
черного цвета, событие
—
коробка окажется с обувью коричневого
цвета,
и
—
несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Сумма ![]() событий
событий ![]() обозначается
так:
обозначается
так:
![]() .
.
Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Произведение событий обозначается
![]() .
.
.
Свойство 1. Если
все случаи являются благоприятствующими
данному событию
,
то это событие обязательно произойдет.
Следовательно, рассматриваемое событие
является достоверным, а вероятность
его появления ![]() ,
так как в этом случае
,
так как в этом случае ![]()
![]()
Свойство
2. Если
нет ни одного случая, благоприятствующего
данному событию
,
то это событие в результате опыта
произойти не может. Следовательно,
рассматриваемое событие является
невозможным, а вероятность его появления ![]() ,
так как в этом случае
,
так как в этом случае ![]() :
:
![]()
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство
4. Вероятность
наступления противоположного
события ![]() определяется
так же, как и вероятность наступления,
события
:
определяется
так же, как и вероятность наступления,
события
:
![]()
где ![]() —
число случаев, благоприятствующих
появлению противоположного события
.
Отсюда вероятность наступления
противоположного события
равна
разнице между единицей и вероятностью
наступления события
:
—
число случаев, благоприятствующих
появлению противоположного события
.
Отсюда вероятность наступления
противоположного события
равна
разнице между единицей и вероятностью
наступления события
:
![]()
|
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
Различные определения вероятностей.
Классическое определение вероятности случайного события.
Вероятность
события ![]() равна
отношению числа благоприятных
событию
исходов
опыта к общему числу исходов опыта.
равна
отношению числа благоприятных
событию
исходов
опыта к общему числу исходов опыта.
![]() , где
, где
![]() -
число благоприятных исходов опыта;
-
число благоприятных исходов опыта;
![]() -
общее число исходов опыта.
-
общее число исходов опыта.
Формулы сложения и умножения вероятностей событий.
Теорема. Вероятность
суммы конечного числа несовместных
событий ![]() равна
сумме вероятностей этих событий
равна
сумме вероятностей этих событий
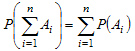
Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место
P(AB) = P(A)×P(B/A) = P(B)×P(A/B).
Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий, т.е.
P(ABC....LM) = P(A)×P(B/A)×P(C/AB) P(M/AB...L).
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
P(A+B) = P(A) + P(B) — P(AB).
Схема Бернулли повторных испытаний. Формула Бернулли.
![]() -
вероятность появления события ровно
-
вероятность появления события ровно ![]() раз
при
независимых
испытаниях,
раз
при
независимых
испытаниях, ![]() -
вероятность появления события при одном
испытании.
-
вероятность появления события при одном
испытании.
Локальная и интегральная формула Лапласа.
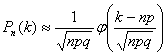 -
вероятность появления события ровно
раз
при
независимых
испытаниях,
-
вероятность появления события при одном
испытании,
-
вероятность появления события ровно
раз
при
независимых
испытаниях,
-
вероятность появления события при одном
испытании, ![]()
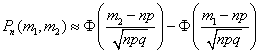 -
вероятность появления события не менее
m1 и
не более m2 раз
при
независимых
испытаниях,
-
вероятность появления события при одном
испытании,
.
-
вероятность появления события не менее
m1 и
не более m2 раз
при
независимых
испытаниях,
-
вероятность появления события при одном
испытании,
.
Закон распределения вероятностей дискретной случайной величины. Числовые характеристики.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.
Таблица соответствия значений случайной величины и их вероятностей вида
x1 |
x2 |
x3 |
... |
xn |
... |
p1 |
p2 |
p3 |
|
pn |
|
Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.
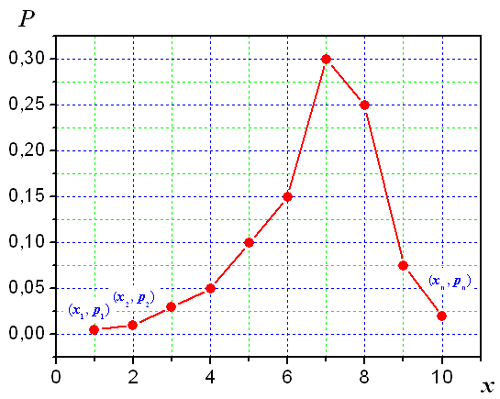
Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует дискретную случайную величину. Однако, когда невозможно определить закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины:
Математическое ожидание,
Дисперсия,
Среднее квадратичное отклонение
Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.

Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.
![]()
Принимая во внимание свойства математического ожидания, легко показать что
![]()
Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число равное
![]()
