
- •Конспект урока. Доли и обыкновенные дроби.
- •Учебник: Математика. 5 класс. Виленкин н.Я., Жохов в.И. И др.
- •Внеклассное мероприятие.
- •Математический квн(5е классы)
- •Ход мероприятия
- •1.Математическая разминка.
- •2.Конкурс капитанов
- •3.Конкурс художников.
- •4.Конкурс « Запоминайка»
- •5.Конкурс «Математическая эстафета»
- •6.Конкурс «Будущие археологи».
ФГБОУ ВПО Нижегородский государственный педагогический университет им. Козьмы Минина
Отчет по педагогической практике
по дисциплине «Теория и методика обучения математике»
Выполнил
студент 4 курса
Группы МИ-10
факультета ЕМКН
Коржавин М.С.
Руководитель:
кандидат педагогических наук, доцент
Огурцова О.К.
г. Нижний Новгород
2013г.
Отчет по педагогической практике в городе Нижнем Новгороде Приокского района МБОУ СОШ №134 5 «Б» класс.
Учитель – Зуева Татьяна Васильевна
Методист – Огурцова Ольга Константиновна
Количественные итоги практики.
Посещено уроков по математике в своем классе – 7
по другим дисциплинам – 17
Дано уроков по математике в своем классе – 15
Замен по математике – 2
Замен по геометрии – 14
Замен по алгебре – 9
Проведено 1 внеклассное мероприятие по математике в 5 «А» и 5 «Б» классах – «Математический КВН».
Изготовлено 5 презентаций по математике и большое количество карточек с заданиями, математическая газета.
Качественные итоги практики
Описание и анализ чужого опыта:
а) описать интересные приемы, формы работы, увиденные в деятельности учителей математики.
В 5 классе при изучении темы «Порядок выполнения действий» учительница использовала в выражениях не только цифры и буквы, но и геометрические фигуры. К примеру, вместо цифр были треугольник, квадрат и кружочек, акцентируя внимание на том, что порядок действия не изменится от используемых величин. так же в 5-м классе, при проведении мной урока на тему "площадь прямоугольника", ученикам был предоставлен раздаточный материал, в виде различных прямоугольников. Метод деятельности был групповой. Им необходимо было из перечня фигур найти те, площади которых равны. Делать это необходимо было совместно. Одна группа предприняли смекалку и пронумеровала фигуры для удобства, а другая решили написать значения площадей на соответствующих прямоугольниках.
б) Анализ урока, проведенного учителем (п.5.5)
1. 11.12.13, 8 «А» класс, школа №134, учитель: Шиповалова Елена Георгиевна.
2. Тема урока: «Площадь трапеции». Это был урок изучения нового, на предыдущих уроках ученики изучили правила нахождения площади параллелограмма. Дидактические единицы – словесное определение параллелограмма, площади, треугольника, . Для учеников эта тема нова, ранее они не встречались с площадью трапеции.
3. Цели урока были сформулированы учителем на мотивационно-ориентировочном этапе. Учебная задача: Сегодня мы с вами научимся находить площадь трапеции, решать задачи.
4. Тип урока – урок изучения нового; методы обучения – репродуктивный, частично-поисковые; форма работы – фронтальная. Средства обучения – традиционные. Методы, формы и средства обучения соответствуют поставленым целям.
Структура урока:
Мотивационно-ориентировочный этап – 15 мин.
Содержательный этап – 20 мин.
Рефлексивно-оценочный этап – 5 мин.
Домашнее задание на уроке не проверялось, т.к. на предыдущем уроке была самостоятельная работа.
Учитель дает подсказки по нахождению площади фигуры, делением ее по частям, а затем предлагает найти площадь трапеции, разделив ее на два треугольника. Вместе с учениками выводят формулу трапеции.
Система упражнений соответствовала поставленным целям урока на всех этапах урока.
В конце урока учитель стал подводить итоги, попросил ученика прочитать определение трапеции, формулу нахождения площади параллелограмма, трапеции, треугольника.. Домашнее задание было записано на доске.
5.План урока выполнен, поставленные цели достигнуты, особое впечатление произвела активная исследовательская работа класса, ребята с удовольствием выполняли задания учителя. Общая оценка урока – отлично.
в) Анализ урока, проведенного студентом (п. 5.5)
1. 02.12.13, 5 «А» класс, школа №134, учитель: Сабурина Екатерина Евгеньевна.
2. Тема урока: Формулы. Тема урока не связана с предыдущим, на предыдущих уроках изучалась тема: Квадрат и куб числа. Дидактические единицы, изучающиеся на уроке – определение. Определение Формулы.
3. Учебная задача: изучить определение формулы ее запись. Была сформулирована учителем на содержательном этапе урока.
4. Тип урока: урок изучения нового, методы: репродуктивный, частично-поисковой, форма обучения: фронтальная, средства обучения: традиционные. Методы, формы и средства обучения соответствуют поставленным целям.
Структура урока:
Мотивационно-ориентировочный этап – 15 мин.
Содержательный этап – 20 мин.
Рефлексивно-оценочный этап – 5 мин.
Домашнее задание не проверялось, т.к. на предыдущем уроке была проведена контрольная работа.
В качестве мотивации были использованы примеры применения формул:
Пути, времени, скорости
Система упражнений и заданий на различных этапах урока соответствовала поставленным целям урока.
Итоги урока были подведены учителем: повторили определение формулы, записи формул пути, времени, скорости.
5. План урока выполнен учителем, поставленные цели достигнуты. На уроке понравилась мотивация, придуманная учителем, а также взаимодействие учителя с учениками. Общая оценка за урок – отлично.
2. Описание и анализ собственного опыта:
а) привести не менее двух наиболее удачных фрагментов собственных уроков;
1. Урок: «Площадь прямоугольного треугольника»
(рассмотрели формулу нахождения площади прямоугольника, вывели самостоятельно формулу нахождения площади прямоугольного треугольника)
Учитель: Скажите мне, пожалуйста, как мы с вами находили площадь прямоугольника?
Ученики: Это произведение длины на ширину.
Учитель: Давайте зарисуем прямоугольник, отметим длину и ширину, а затем разделим его пополам. равны ли у нас площади фигур, если мы разделили пополам?
Ученики: Да, мы делили пополам, по этому, площади равны.
Учитель: Все верно, а можем ли мы разделить прямоугольник, соединив противоположные вершинки? Равные ли фигурки у нас получатся?
Ученики: Да, можем, фигурки получились равны.
Учитель: Все правильно, а теперь найдем площадь каждой фигурки, если мы знаем как находить площадь прямоугольника.
Ученики: Нужно площадь прямоугольника разделить пополам.
Учитель: Площадь какой фигуры мы нашли?
Ученики: Треугольника
Учитель:
Запишем в тетрадочки: Площадь прямоугольного
треугольника S=
 (a*b)
(a*b)
Тема: «Объем»
Учитель: -Посмотрите на эту фигуру. Она разделена на кубики, стороны которых равны 1 см. Как вы думаете, как можно найти объем этой фигуры?
Ученики: Посчитать количество кубиков.
Учитель:
Все
верно, Так мы и найдем объем этой фигуры.
объем одного маленького кубика, на
которые мы разбивали нашу фигуру называют
кубическим сантиметром и пишут, что она
равна 1
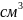 ,
значит
чему равен
объем всей нашей фигуры?
,
значит
чему равен
объем всей нашей фигуры?
Ученики: 8
Учитель: Тогда, скажите мне как найти объем параллелепипеда?
Ученики: Надо разбить его на кубики с ребрами 1 см и посчитать их
Учитель: Давайте тогда нарисуем в тетради параллелепипед со сторонами 6, 4 и 2 см, разделим его на кубики и найдем площадь.
Ученики: Чертят, подсчитывают кубические сантиметры. Получается 48 см2
Учитель: как найти объем, не разделяя каждый раз фигуру?
Ученики: не знаем
Учитель: Вот сегодня мы и узнаем с вами как находить объем более быстрым и удобным способом.
б) выявить причины неудавшихся моментов уроков.
Основными причинами неудавшихся моментов на уроках являлись:
недостаточное продумывание урока, точнее вопросов учителя и возможных ответов учеников;
недостаточно продуманная актуализация урока;
иногда были рассмотрены не все возможные способы решения задачи;
отсутствие опыта, неумение вести себя в экстренных, затруднительных ситуациях.
Отразить положительные и отрецательные стороны проведенных внеклассных мероприятий по математике.
Положительные стороны проведенного внеклассного мероприятия по математике: у учеников активно работало логическое мышление, одно из заданий было на последнюю пройденную тему, что помогло закрепить материал, научились работать в команде, получили дополнительные оценки, небольшие призы, грамоты и хорошее настроение.
Отрицательные стороны проведенного внеклассного мероприятия по математике: на внеклассное мероприятие был отведен всего лишь урок, что очень мало для подобной игры, иногда ученики не справлялись с заданием, ученики нарушали дисциплину и не всегда получалось быстро их угомонить, а некоторые очень расстраивались, если подводили команду.
Проанализировать использование материалов, полученных на занятиях по кафедрам факультета, а также по кафедрам педагогики, психологии, физиологии.
Полученные знания в университете очень помогли на практике, как по математике, так и по педагогике и психологии.
Используя все знания, я составляла уроки, используя технологию развивающего обучения, урок старалась делить на три основных этапа – мотивационно-ориентировочный, содержательный и рефлексивно-оценочный, что способствовало наиболее эффективному усвоению темы урока.
Знания по другим предметам помогли найти подход к каждому ученику, так же к классу вцелом.
Выводы
Практика дала мне большой опыт в работе учителем. Помогла научить ставить цели перед уроком, искать пути их решения. Так же я получил огромный социальный опыт в общении с детьми, с учителями. Было интересно почувствовать себя в роли учителя, очень приятно было видеть, что они понимают и успешно применяют то, что мы им объясняли, спрашивают, когда появляются вопросы.
Предложение: сделать пассивную практику со второго курса.
Конспект урока. Доли и обыкновенные дроби.
Тип урока: комбинированный урок изучения нового материала и параллельного решения задач.
Учебник: Математика. 5 класс. Виленкин н.Я., Жохов в.И. И др.
Учебная задача: узнать с учениками, что такое доли и обыкновенные дроби, что такое половина, треть, четверть, числитель, знаменатель, параллельно закрепляя знания элементарными задачами.
Диагностируемые цели: В результате урока ученик:
- знает что такое доли и обыкновенные дроби, что они обозначают, что обозначает числитель, а что знаменатель, что такое половина, треть, четверть.
- умеет правильно их читать, записывать и решать самые элементарные задачи с ними.
Методы обучения: репродуктивный, УДЕ
Форма работы: фронтальная
Средства обучения: традиционныя, презентация, раздаточный и наглядный материал.
Структура урока:
-Мотивационно-ориентировочный этап (10 мин)
-Содержательный этап (27 мин)
-Рефлексивно-оценочный этап (3 мин)
Ход урока
Название этапа |
Действия учителя |
Действия учеников |
Записи в тетради |
Актуализация |
-Запишем число, сегодня 17 декабря, Классная работа. Смотрим на интерактивную доску, сосчитаем, сколько у нас арбузов на доске? Первый слайд Второй слайд Третий слайд Четвертый слайд Пятый слайд Как называются такие числа? Действительно, мы получаем натуральные числа. |
Считают
1 2 3 4 5 Натуральные числа |
|
Мотивация |
Задача 1. Смотрим на доску. AB=6 условных единиц, CD=2 условные единицы. Как мы выразим отрезок AB через CD? Задача2. Решаем следующую задачу. AB=7 условных единиц CD=2 условные единицы Можем ли мы найти AB? Действительно, мы не можем выразить AB натуральным числом. Значит должны существовать не только натуральные числа. -хорошо, смотрите, у нас есть один мандарин и 5 человек, мы можем поделить мандарин поровну для 5х человек, чтобы никого не обидеть? -так значит, получается, можем мы один мандарин разделить между пятью людьми? -каждый из нас в повседневной жизни сталкивается с тем, что нам нужно что-то одно разделить на части, вот мы сегодня на уроке и узнаем как называются эти части и что они показывают |
AB=3CD
нет
-да, разрежем на 5 равных частей
-да
|
|
Содержательный этап |
-мы с вами говорили о дольках мандарина, о «дольках» торта. Как вы думаете, как будет называться тема нашего урока? -Очень похоже, но назовем мы более научно- Доли и познакомимся с понятием обыкновенные дроби, итак, откройте тетради и запишите число, сегодня 17 декабря, классная работа. Тема урока: Доли и дроби -Так вот, представим теперь, что у нас есть арбуз и семья, состоящая из: мамы, папы, двух детей и бабушки с дедушкой. Мама разрезала этот арбуз на 6 равных частей- как вы видите, для каждого члена семьи . Как мы с вами ранее выяснили называются эти части? -Давайте теперь запишем определение доли: -Доля – одна из равных частей единицы. Так как арбуз разрезали на 6 равных частей, значит его разделили на 6 долей и каждый получил «одну шестую» долю арбуза, или, короче «одну шестую арбуза». -Давайте также запишем, что: Для записи любой доли используют горизонтальную чёрточку. Её называют дробной чертой И
пишут
-скажите, какое у нас число стоит под чертой и что оно у нас означает? -верно, значит получается, что число под чертой показывает на сколько равных частей (долей) разделили единицу. Запишем это. -а если мы разделим наш арбуз пополам, т.е на 2 доли, 1 доля –это что у нас будет? -правильно. Самая известная доля – это, конечно, половина. Слова с приставкой «пол» можно услышать часто: полчаса, полкилометра… Разделили целое на две равные части – «половина».половина у нас записывается как . запишите какую долю называют половиной -Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на три части – «треть». Треть
у нас записывается как
-как
вы думаете, а если разделим на 4 части,
то как будем называть?
-Итак,
получается долю
-а если на 5 или 6 разделим, то как будем говорить? Так вот слов, аналогичных «треть» и «четверть» в русском языке нет, поэтому чтобы назвать доли пользуются словами «пятая», «шестая». Запишем это
-теперь давайте рассмотрим нашу задачу. Найдите длину отрезка AB, если в качестве единичного от- резка выбран отрезок CD AB
=
Сколько взялми равных частей? На сколько равных частей разделили ? А теперь третью задачу: Найдите длину отрезка CD, если в качестве единичного от- резка выбран отрезок AB CD
=
рассмотрим
долю
и запишем: Запись такого вида называют
обыкновенной дробью. В дроби числитель и знаменатель отделяются друг от друга дробной чертой. Знаменатель показывает, на сколько долей делят, а числитель – сколько таких долей взято. При чтении дробей надо помнить: числитель дроби – количественное числительное женского рода (одна, две, восемь и т.д.), а знаменатель – порядковое числительное (седьмая, сотая, двести тридцатая и т.д.) Например: одна пятая, две шестых; -о дроби можно запомнить по такому стишку: Каждый может за версту Видеть дробную черту. Над чертой – числитель, знайте, Под чертою – знаменатель. Дробь такую, непременно, Надо звать обыкновенной.(раздается перед уроком напечатанный) -При чтении дробей надо помнить: числитель дроби – количественное числительное женского рода (одна, две, восемь и т.д.), а знаменатель – порядковое числительное (седьмая, сотая, двести тридцатая и т.д.) -задание: Запишите в виде обыкновенной дроби:
Далее номера по учебнику :884(какая часть фигуры закрашена), 885(начертить треть квадрата), 886( разделить квадрат разными способами на 4 доли), 888(прочитать дроби) |
-могут сказать дольки или что-то похожее
-доли
-6, это на сколько частей разделили арбуз
-1 половина
-предположения, может кто-то правильно назовет
-говорят предположения
7
2
-выполняют |
-доли и обыкновенные дроби
-Доля – каждая из равных частей единицы. Так как арбуз разрезали на 6 равных частей, значит его разделили на 6 долей и каждый получил «одну шестую» долю арбуза, или, короче «одну шестую арбуза».
- Для записи любой доли используют горизонтальную чёрточку. Её называют дробной чертой И пишут арбуза
- число под чертой показывает на сколько равных частей (долей) разделили единицу.
- долю называют половиной
- долю называют «треть»
- долю называют «четверть»
-далее, чтобы назвать доли пользуются словами «пятая», «шестая»
- Запись вида называют обыкновенной дробью. В дроби : 2-числитель, 7-знаменатель, числитель и знаменатель отделяются друг от друга дробной чертой. Знаменатель показывает, на сколько долей делят, а числитель – сколько таких долей взято.
|
Рефлексия |
Какова была цель урока? Достигли? С какими понятиями познакомились? Что такое доля? Что такое дробь? Где у дроби знаменатель? где числитель?
д/з: 896, 897, 900, 901 |
- узнать как правильно называются эти части, уметь правильно эти части выделять и называть их, да -доли,дроби - Доля – каждая из равных частей единицы. - Запись вида называют обыкновенной дробью. -знаменатель внизу, числитель сверху |
|

 арбуза
арбуза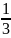 .
запишите какую долю называют «треть»
.
запишите какую долю называют «треть»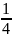 называют «четверть». Запишем это
называют «четверть». Запишем это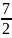
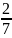
 : 2-числитель, 7-знаменатель.
: 2-числитель, 7-знаменатель.