Модуль 2. Продольная устойчивость автомобилей и колёсных тракторов Лекция 2.1. Кинематика и динамика колёс

2.1.1. Классификация колёс автомобилей и тракторов

Прежде чем приступить к изучению закономерностей движения автомобиля и трактора, необходимо рассмотреть основные зависимости, связанные с работой одного из их важнейших устройств – колеса.

Можно выделить две группы режимов качения колеса, определяемых следующими факторами:

- способом привода колеса во вращение (ведомое, ведущее, тормозящее);

- физико-механическими свойствами поверхности качения и колеса.

Колесо считают ведомым, если оно катится под действием толкающей силы, приложенной к оси колеса. Колесо приводится во вращение моментом, который образуется толкающей силой и силой трения обода с поверхностью качения на плече, равном радиусу колеса.

Колесо называют ведущим, если оно катится под действием крутящего момента, передаваемого трансмиссией машины.

Колесо считают тормозящим, если оно подвержено действию тормозного момента, приложенного к ступице.

В зависимости от конструкции колеса и характера поверхности его качения различают следующие варианты режимов качения колеса:

- качение колеса с жёстким ободом по недеформируемой поверхности. Примером может служить качение опорных катков по гусенице;

- качение колеса с жёстким ободом по деформируемой поверхности. К этому варианту можно отнести с некоторым допущением равномерное качение без вертикальных колебаний колеса, с пневматической шиной высокого давления по слабо несущему грунту;

- качение эластичного колеса по недеформируемой поверхности. С некоторым допущением это качение пневматической шины низкого давления по дороге с твёрдым покрытием;

- качение колеса с эластичным ободом по деформируемой поверхности. Это наиболее типичный случай в эксплуатации сельскохозяйственных тракторов.

2.1.2. Качение колеса с жёстким ободом по деформируемой поверхности

Рассмотрим процесс возникновения силы сопротивления качению ведомого колеса из-за смятия почвы. Для этого используем известный диалектический приём: абстрагируемся от некоторых реальных особенностей колеса и почвы, которые пока будем считать несущественными.

Допустим, что колесо и почва идеальные, т.е. они характеризуются следующим:

- колесо абсолютно жёсткое и без почвозацепов;

- колесо катится по горизонтальной поверхности почвы равномерно и без скольжения (ведомое колесо);

- на оси колеса момент трения в подшипниках равен нулю;

- в почве под колесом образуются только остаточные деформации;

- сопротивлением воздуха при качении колеса можно пренебречь.

Такое колесо представлено на рисунке 12. С учётом принятых допущений составим условия равновесия колеса, на которое действует нормальная нагрузка - со стороны остова машины; толкающая сила остова - и равнодействующая реакций почвы - .

Известно, что если тело (колесо) находится в состоянии равномерного движения под действием трёх сил, то направления действия этих сил пересекаются в одной точке. Так как силы и приложены к оси колеса, то и направление действия реакции проходит через центр колеса.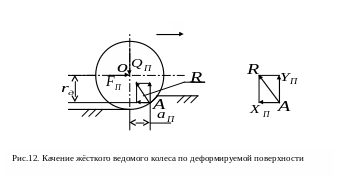

Из этого следует два важных вывода: 1) элементарные реакции почвы направлены по радиусу жёсткого колеса нормально к ободу колеса; 2) реакция почвы приложена в точке контакта колеса с почвой на некотором расстоянии от вертикальной его оси.

Разложим равнодействующую на нормальную и горизонтальную составляющие. Последнюю назовём силой сопротивления качению ведомого колеса, так как она действует против направления движения. Плечо действия силы обозначим через (динамический радиус колеса). Тогда условия равновесия ведомого колеса будут такие:

; ;

; ;

,

где - момент сопротивления качению ведомого колеса; - коэффициент сопротивления качению ведомого колеса.

Проанализируем полученные выражения. Нормальная составляющая реакции почвы равна нормальной нагрузке на ось колеса, но приложена не по вертикали (по нормали) к оси колеса, а смещена по ходу движения на величину . Для жёсткого колеса зависит не только от свойств и состояния почвы, но и от ширины колеса.

Коэффициент сопротивления качению прямо пропорционален плечу и обратно пропорционален динамическому радиусу . Следовательно, для уменьшения силы сопротивления качению ведомого колеса следует уменьшать нагрузку , плечо и увеличивать радиус колеса .

Для оценки значений коэффициента сопротивления качению ведомого колеса по почве в процессе опытов можно использовать выражение , в котором силы и замеряют динамографом, учитывая что .

2.1.3. Пневматические шины. Виды деформаций шины. Радиусы пневматической шины.

Пневматическую шину широко применяют главным образом благодаря её амортизирующим свойствам. Она значительно смягчает толчки от неровностей дороги, передаваемые водителю и корпусу машины. Это свойство особенно важно для сельскохозяйственных тракторов, работающих в условиях бездорожья и в большинстве своём не имеющих подвески. Под действием внешних нагрузок пневматическая шина подвергается различным видам деформаций, которые взаимосвязаны между собой. Различают четыре вида деформации пневматической шины:

- нормальная или радиальная деформация шины происходит под действием нормальной нагрузки . Между шиной и опорной поверхностью создаётся площадь контакта (см. рис. 13).

Величина называется нормальной деформацией шины. Различают радиальные деформации отдельных точек беговой дорожки шины, определяемые как разность между свободным радиусом колеса и радиусом соответствующей точки.

Отношение называется средним (приведённым) коэффициентом жёсткости шины в нормальном направлении. Коэффициент является одним из наиболее важных параметров шины. Его величина зависит главным образом от давления воздуха в шине (чем меньше давление, тем больше нормальная деформация шины и меньше коэффициент ) и от размеров, конструкции и материала шины. Коэффициент не является величиной постоянной и по мере увеличения нагрузки деформация растёт всё более медленно;

- тангенциальная или окружная деформация шины возникает под действием крутящего момента , который вызывает деформирование боковин и протектора шины. Вследствие этого обод колеса поворачивается на некоторый угол закрутки . Соотношение между крутящим моментом и деформацией шины, измеряемой углом закрутки , характеризует её жёсткость в окружном направлении. Жёсткость шины в окружном направлении определяется как отношение крутящего момента к величине угла закрутки ;

- поперечная (боковая) деформация шины возникает под действием боковой силы и существенно влияет на устойчивость и управляемость машины. Действие боковой силы (см. рис.14) вызывает так называемый увод шины, который выражается в том, что колесо отклоняется от первоначального направления движения и начинает двигаться под некоторым углом к нему.

Угол называется углом бокового увода, а отношение называется коэффициентом сопротивления боковому уводу. На сопротивление шин боковому уводу оказывает влияние конструкция и размеры шины и величина давления воздуха в них. Эта зависимость справедлива лишь до тех пор, пока боковой увод происходит без бокового скольжения шины. Для современных легковых автомобилей углы увода не превышают 3…5 градусов и ещё меньше для грузовых автомобилей и тракторов. При углах больше указанных наступает быстро прогрессирующее боковое скольжение шины, которое превращается в занос, когда боковая сила сцепления шины с дорогой используется полностью;

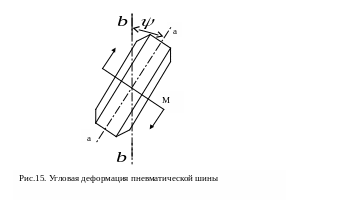
- угловая деформация шины возникает, если к колесу, нагруженному нормальной силой, приложить момент , параллельный поверхности пути. Угловая деформация шины проявляется в том (см. рис15), что средняя линия протектора отклоняется на некоторый угол от средней линии площади контакта шины с дорогой. Отношение момента к углу характеризует угловую жёсткость шины. Благодаря угловой податливости шины колесо может в некоторых пределах отклоняться от направления своего движения без заметного проскальзывания элементов протектора относительно дороги. Однако при дальнейшем росте момента начинается скольжение шины и угол прогрессивно растёт.

В связи с различными деформациями, которым подвергается пневматическая шина, радиус её не имеет единственного определённого значения, о каком можно говорить применительно к жёсткому колесу.

Различают следующие радиусы колеса, снабжённого пневматической шиной: свободный , статический , динамический (теоретический) и кинематический .

Свободный радиус - это радиус беговой дорожки колеса, свободного от внешней нагрузки. Он равен расстоянию от поверхности беговой дорожки до оси колеса. Значения свободного радиуса колеса зависит от давления воздуха в шине.

Статический радиус представляет собой расстояние от оси неподвижного колеса, нагруженного нормальной нагрузкой, до плоскости его опоры. При этом оговаривают, чему равна нагрузка, действующая на колесо, каково давление воздуха в шине и что собой представляет опорная поверхность колеса.

Динамический радиус - это расстояние от оси движущегося колеса до точки приложения результирующей элементарных реакций почвы, действующих на колесо.

Кинематическим радиусом колеса называется радиус такого фиктивного колеса с жёстким ободом, которое вращаясь с той же угловой скоростью, что и действительное колесо и двигаясь без буксования и скольжения, имело бы такую же поступательную скорость, какую имеет действительное колесо. Кинематический радиус колеса определяет путь, пройденный колесом за один оборот.