Лекция 1.3. Типы поверхности пути и определение характеристик воздействия при движении автомобиля и трактора по неровностям пути

1.3.1. Геометрические свойства поверхности пути

Геометрия поверхности пути оказывает большое влияние на динамические и тяговые свойства автомобиля и трактора. Поверхность пути можно представить в виде совокупностей неровностей различной высоты и формы.

Если высота и форма неровностей поверхности пути соизмерима с размерами автомобиля и трактора или превышает их, такую поверхность можно отнести к макропрофилю (подъёмы, уклоны, холмы, ложбины), если же меньше, то такую поверхность следует отнести к микропрофилю (продольные борозды, поверхность при междурядной обработке пропашных культур, мелкие выбоины дороги, кочки и т.п.).

Макропрофиль поверхности оказывает в основном влияние на проходимость и устойчивость автомобилей и тракторов. Размеры и формы препятствий могут быть самыми разнообразными, однако можно ограничиться рассмотрением нескольких типовых препятствий. Потеря проходимости может быть вызвана двумя причинами: зависание машинно-тракторного агрегата на препятствии из-за недостаточного клиренса и упором носовой части автомобиля и трактора в препятствие из-за недостаточного угла атаки.

Препятствие описывается полностью, если приведены все размеры профиля, однако по рекомендациям профессора М.Г.Беккера все формы препятствий с некоторыми допущениями сведены к канаве и насыпи в виде прямоугольников с размерами «h» и «b».

Поперечная и продольная устойчивость агрегата на склоне определяется углами подъёма и уклона и будет рассмотрена более подробно позднее. Следует заметить, что геометрию поверхности пути с точки зрения проходимости и устойчивости всегда увязывают с размерами агрегата. То, что непроходимо для одного вида агрегата, может быть проходимо для другого.

Микропрофиль поверхности в виде часто повторяющихся неровностей вызывает колебательные процессы в агрегате, что приводит к ухудшению условий работы водителя, увеличению нагруженности деталей и узлов машины, снижению скорости движения, управляемости и устойчивости.

Как правило, неровности носят случайный характер. Даже такие неровности, как поливные борозды, междурядья, пахотные борозды и другие, которые образованы в результате взаимодействия почвы с рабочими органами, не имеют строго точных геометрических форм. Это происходит потому, что свойства почвы от участка к участку не постоянны, скорость обработки и характер взаимодействия рабочих органов с почвой колеблются в некоторых пределах, а также влияют атмосферные осадки и т.д. Тем более не имеют постоянных характеристик грунтовые дороги, стерня, просёлочные дороги, микропрофиль которых образуется в результате воздействия случайных факторов. На рис.3 представлена профилограмма почвы двухлетней залежи.

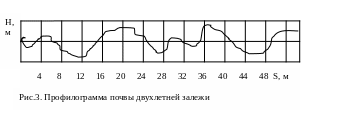
1.3.2. Определение характеристик воздействия при движении автомобиля и трактора по неровностям пути

Для описания характеристик воздействия на автомобиль или трактор при движении по неровностям пути в последнее время широко применяют вероятностные методы теории случайных величин, а для более полной оценки теорию случайных функций.

Движение автомобиля или трактора по микропрофилю можно рассматривать как эргодический стационарный процесс, который не зависит от того, начнёт ли движение машина по данному микропрофилю и с определённой скоростью в настоящий момент или через какое-то время. В этом случае эргодическая стационарная случайная функция воздействия зависит только от свойств микропрофиля и скорости движения. Кроме того из теории случайных функций известно, что если случайный процесс стационарный, то его основные характеристики математическое ожидание и дисперсия являются постоянными величинами и не зависят от времени.

Коль скоро это так, то если дискретная случайная величина H имеет возможные значения с вероятностями , то математическое ожидание определяется по формуле:

.

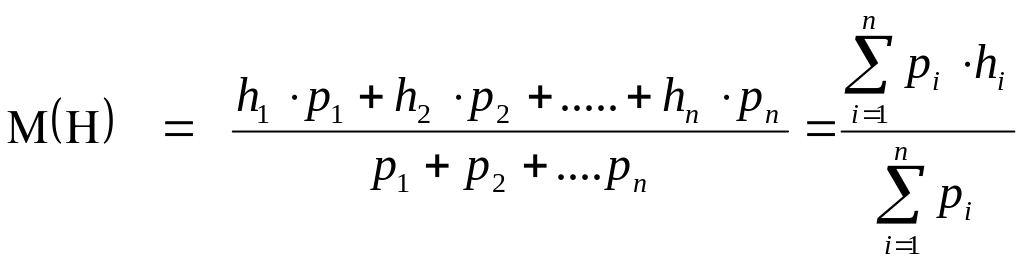Таким образом, рассматривая движение автомобиля или трактора по микропрофилю пути как эргодический и стационарный процесс, мы можем констатировать, что математическое ожидание воздействия зависит только от микропрофиля пути и не зависит от скорости движения по нему.

Дисперсия дискретной случайной величины D(H) определяется по формуле:

.

Аналогично математическому ожиданию, дисперсия воздействия также зависит только от микропрофиля пути и не зависит от скорости движения автомобиля и трактора по нему.

Для того чтобы оценить влияние скорости движения автомобиля и трактора на величину воздействия вводят характеристики случайных процессов, такие как корреляционная функция и спектральная плотность (спектр частот).

Корреляционную функцию для каждого режима движения определяют по микропрофилю пути. Эта функция является основной статистической характеристикой во временной области стационарного случайного процесса и отражает все основные свойства воздействия: характер неровностей микропрофиля пути (высоту, форму и длину) и скорость движения машины по нему.

Корреляционная функция характеризует связь между ординатами случайной функции воздействия, смещёнными друг относительно друга на время . Перевод случайной функции H(S) микропрофиля пути в случайную функцию воздействия H(t) осуществляется заменой переменной в соответствии с зависимостью , где - скорость движения машины.

Для случайной функции H(t) корреляционная функция записывается в следующем виде:

,

где - разность моментов времени, в которые наблюдались ординаты случайной функции Н(t);

- текущее значение времени.

Из формулы видно, что при нулевом смещении значение корреляционной функции будет равно дисперсии ординат неровностей микропрофиля пути .

При , но малом, значения ординат H(t) и H(t+ ) мало отличаются друг от друга. Таким образом, если величина H(t) приняла какое-то значение, то и величина H(t+ ) с большой вероятностью примет значение близкое к нему. При =0 связь будет наибольшей. При увеличении сдвига зависимость ординат H(t) и H(t+ ) между собой должна слабеть и, следовательно, значение должно уменьшаться. Поэтому всегда справедливо неравенство .

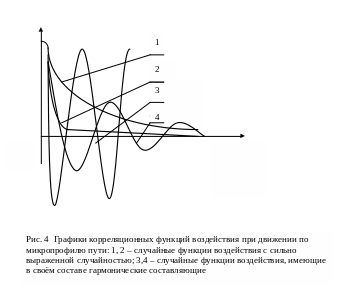
Если микропрофиль пути представляет собой гармоническую функцию (например, синусоидальную или косинусоидальную), то корреляционная функция такого воздействия представляет собой гармоническую функцию той же частоты, что и функция воздействия. На рис.4 приведены корреляционные функции различных случайных функций воздействия.

Из рисунка видно, что , выраженная кривой 1 характеризует случайную функцию воздействия без гармонических составляющих, т.к. значение непрерывно убывает с увеличением значений , и отсутствуют периодические колебания значений . Кривая 2 также не имеет гармонических составляющих, но степень случайности процесса воздействия здесь существенно выше, т.к. значение резко уменьшается с увеличением значений . Кривые 3 и 4 характеризуют процесс воздействия, в котором явно присутствуют гармонические составляющие, при этом кривая 3 описывает процесс воздействия с малой случайностью и высокой периодичностью, т.е. процесс близкий к обычному гармоническому процессу. Кривая 4 описывает процесс воздействия со случайными и периодическими составляющими.

Пример построения корреляционной функции и её аппроксимации даётся в книге И.Б.Барского и др. «Динамика трактора», М. Машиностроение, 1973г., 280с.

Несмотря на большую универсальность и общность корреляционных функций как характеристик случайных процессов, в практических исследованиях также широкое применение находят спектральные характеристики, в частности спектральная плотность.

Спектральная плотность характеризует непрерывный спектр имеющихся частот в данной случайной функции воздействия. На рис.5 приведен график спектральной плотности.

Спектральная плотность и корреляционная функции связаны между собой зависимостью

.

Можно получить и обратную зависимость корреляционной функции от спектральной плотности:

.

Если имеются графики корреляционной функции, аналогичные изображённым на рисунке 4, то можно подобрать аналитическое выражение этой функции

,

где - неопределённые коэффициенты; .

При обработке функций воздействия можно найти такие значения коэффициентов , при которых можно получить достаточно точный график корреляционной функции.

Если, например, спектральная плотность имеет резко выраженный один max, то случайная функция воздействия содержит в основном частоты близкие к одной частоте соответствующей max функции спектральной плотности. Если спектральная плотность является пологой кривой, то случайная функция воздействия содержит примерно в равной мере весь спектр частот.

Спектральная плотность случайной функции воздействия используется при моделировании динамики автомобилей и тракторов, а также при моделировании нагрузки при стендовых испытаниях машин.