Возрастание и убывание функции на интервале.

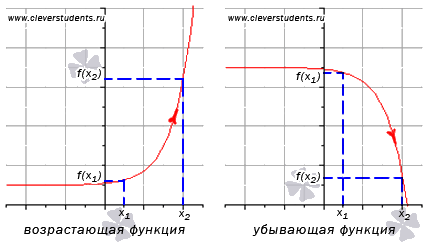
Определение возрастающей функции.

Функция y=f(x) возрастает на интервале X, если для любых   и  выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y=f(x) убывает на интервале X, если для любых   и  выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.

К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале   мы можем утверждать о возрастании на отрезке  .

31-32.определение экстремума

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство (f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ^'(x)  0

(f ^' (x)  0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) ≤f(x_о) (f(x) ≥ f(x_о)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Точки экстремума

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ^'(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ^' (x) при переходе через точку x_о меняет знак плюс на минус, то в точкеx_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную  f ^' (x) в окрестности точки x_о и вторую производную   в самой точке x_о. Если f ^' (x_о) = 0,  >0 ( <0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же  =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 3.22. Найти экстремумы функции f(x) = 2x³ - 15x²+ 36x - 14.

Решение. Так как f ^'(x) = 6x² - 30x +36 = 6(x -2)(x - 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции в точках x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

33. наибольшее и наименьшее значение функции на отрезке

Если функция   определена и непрерывна на отрезке   , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение   функция   принимает в точке  , то   будет локальным максимумом функции  , так как в этом случае существует окрестность точки  , такая, что   .

Однако свое наибольшее значение   функция   может принимать и на концах отрезка   . Поэтому, чтобы найти наибольшее значение   непрерывной на отрезке   функции  , надо найти все максимумы функции на интервале   и значения   на концах отрезка  , то есть   и  , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.

Наименьшим значением   непрерывной на отрезке   функции   будет наименьший минимум среди всех минимумов функции   на интервале   и значений   и  .

Пример

Задание. Найти наибольшее и наименьшее значение функции   на отрезке  .

Решение. Находим производную функции:

Находим точки, в которых производная равна нулю:

Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку  . Оба значения лежат в этом промежутке.

Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:

Таким образом,

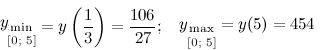
Ответ. 

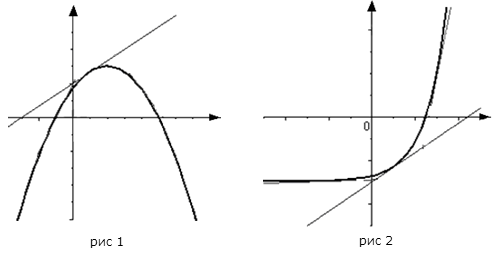
34-35. График функции  , дифференцируемой на интервале  , является на этом интервале выпуклым, если график этой функции в пределах интервала   лежит не выше любой своей касательной (рис. 1).

График функции  , дифференцируемой на интервале  , является на этом интервале вогнутым, если график этой функции в пределах интервала   лежит не ниже любой своей касательной (рис. 2).