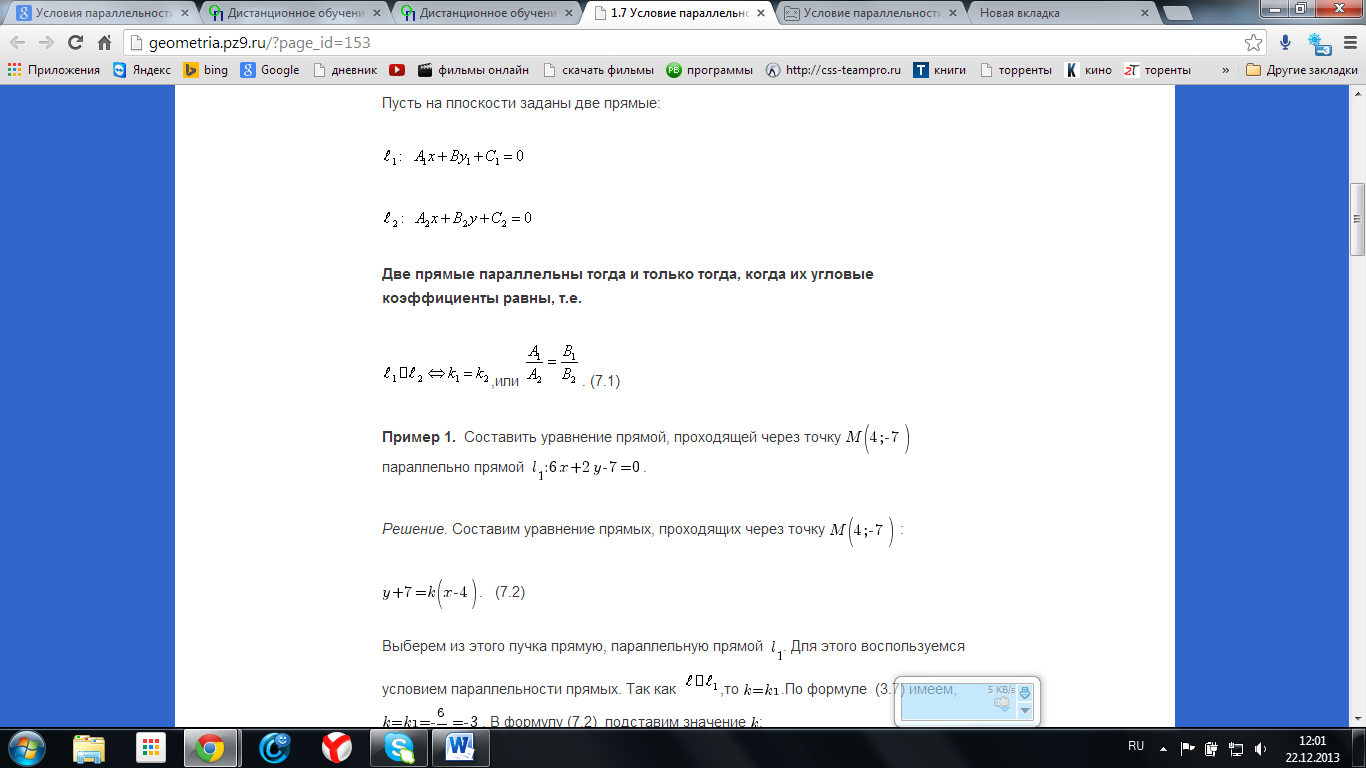
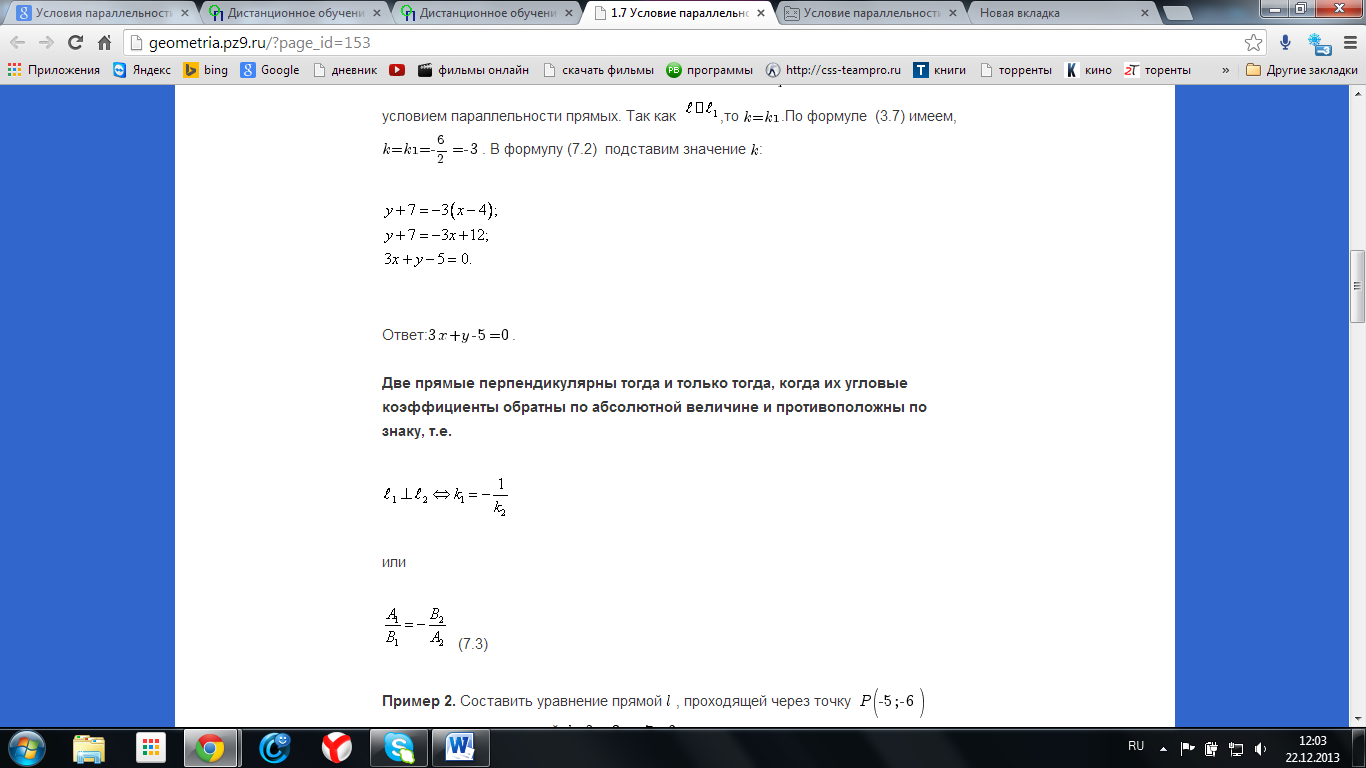
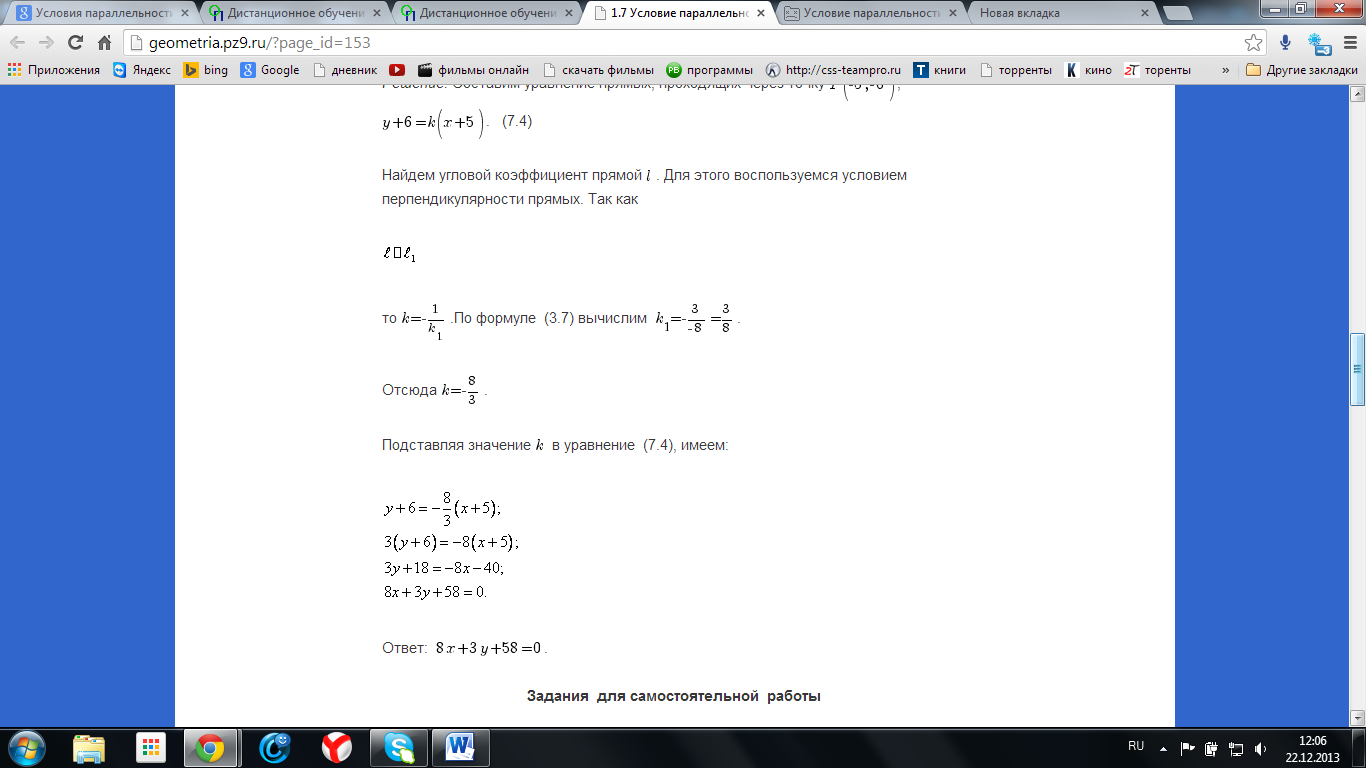
11. Условие параллельности и перпендикулярности прямых

12. Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Если прямая параллельна плоскости проекции, например (h || П₁), то для того чтобы определить расстояние от точкиА до прямой h необходимо опустить перпендикуляр из точки А на горизонтальную прямую h (рис. 4.7).

На ортогональном чертеже в соответствии с теоремой о проецировании прямого угла, строим отрезок A₁M₁, перпендикулярно h₁. Длину перпендикуляра АM можно найти способом прямоугольного треугольника. Откладываем отрезок |M₁M₀ равный |A₂B₂|; тогда |АM| = |А₁M₀|.

Рассмотрим более сложный пример, когда прямая занимает общее положение. Пусть необходимо определить расстояние от точки М до прямой а общего положения (рис. 4.8).

Решение задачи проводим в соответствии со следующим алгоритмом:

1. Через заданную точку M проводим плоскость перпендикулярную заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h):  = h   f.

2. Находим точку пересечения (K) исходной прямойа с плоскостью , для чего вводим плоскость-посредник , проходящую через прямую а (a₁  ₁). Отрезок MK и будет определять расстояние от точки M до прямой a

3. Находим расстояние от точки М до точки Kспособом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M₂K₂N₂равна расстоянию от точки M до прямой а: |MK| = M₂N₂.

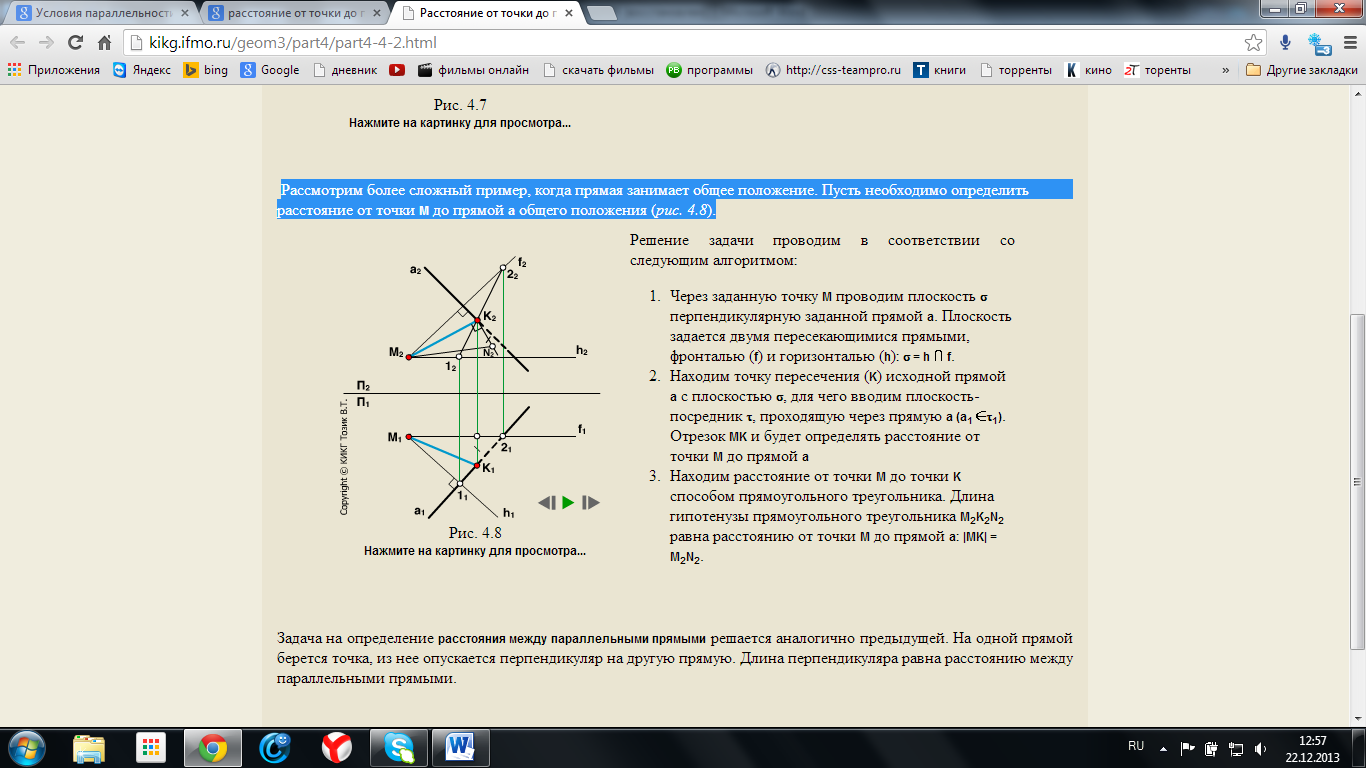
Задача на определение расстояния между параллельными прямыми решается аналогично предыдущей. На одной прямой берется точка, из нее опускается перпендикуляр на другую прямую. Длина перпендикуляра равна расстоянию между параллельными прямыми.

13. Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.

 

Уравнение окружности радиуса  R  с центром в точке О ( х₀ ,  у ₀ ) имеет вид:

 

( х – х₀ ) ²  + ( у – у ₀ ) ² = R ² .

 

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

 

х ²  +  у  ² = R ² .

 

Пусть  Р ( х₁ ,  у ₁ ) – точка окружности ( рис.1 ), тогда  уравнение касательной к окружности в данной точке имеет вид:

 

( х₁ – х₀ ) ( х – х₀ )  + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

 

Условие касания прямой  y = m x + k  и окружности  х ²  +  у  ² = R ² :

 

 

k 2  / ( 1 + m ² ) = R ² .

Основные формулы

Длина окружности:

Радиус окружности:

Диаметр окружности:

Площадь круга радиуса R:

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

14. Эллипс

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами   и  , расстояние между ними - через 2с. По определению эллипса   или  .

Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид

 (1)

где  ; очевидно,  . Уравнение вида (1) называется каноническим уравнением эллипса.

При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае  ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.

Число

где а - большая полуось, называется эксцентриситетом эллипса. Очевидно,   (для окружности  ). Если М(x; y) - произвольная точка эллипса, то отрезки   и   (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам

,  .

Если эллипс определен уравнением (1) и  , то прямые

, 

(рис.) называются директрисами эллипса (если  , то директрисы определяются уравнениями  ,  .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:

Если две плоскости   и   образуют острый угол  , то проекциейй на плоскость   окружности радиуса a, лежащей на плоскости  , является эллипс с большой полуосью а; малая полуось b этого эллипса определяется по формуле

(рис.).

Если круглый цилиндр имеет в качестве направляющей окружность радиуса b, то в сечении этого цилиндра плоскостью, наклоненной к оси цилиндра под острым углом  , будет эллипс, малая полуось которого рвна b; большая полуось а этого эллипса определяется по формуле

(рис.).

15. Гипербола

16. Парабола