Линейные преобразования[править | править исходный текст]
Основная статья: Линейное отображение
Рассмотрим линейное
преобразование 
,
действующее из
-мерного
векторного пространства 
в
-мерное
векторное пространство 
,
имеющее следующий вид:
.
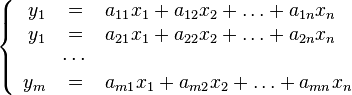В матричной форме это преобразование уравнения вида:
.
Матрица — это матрица коэффициентов линейного преобразования.
Если
рассмотреть действие линейного
преобразования 
на
векторы вида
,
составляюще
базис пространства
,
то 
—
это есть j-ый
столбец матрицы
.
Таким образом, матрица полностью описывает линейное преобразование , и, поэтому, называется матрицей линейного преобразования.
6. Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощьюэлементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.
7. формула крамера
Описание метода
Для системы линейных уравнений с неизвестными (над произвольным полем)
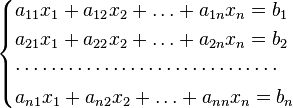
с
определителем матрицы системы 
,
отличным от нуля, решение записывается
в виде
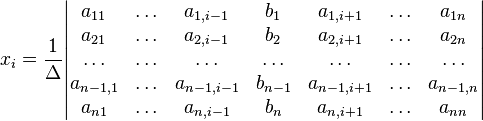
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
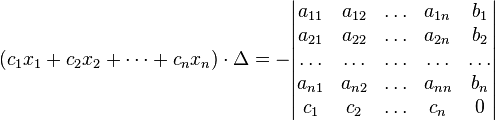
В
этой форме формула Крамера справедлива
без предположения, что
отлично
от нуля, не нужно даже, чтобы коэффициенты
системы были бы элементами целостного
кольца(определитель
системы может быть даже делителем нуля
в кольце коэффициентов). Можно также
считать, что либо наборы 
и 
,
либо набор 
состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
Пример
Система линейных уравнений:
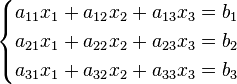
Определители:
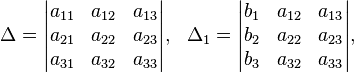
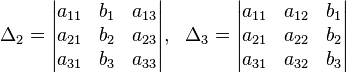
Решение:
Пример:
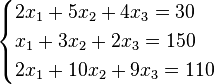
Определители:
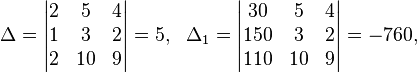
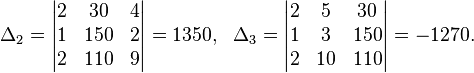
8. Метод Гаусса
Пусть исходная система выглядит следующим образом
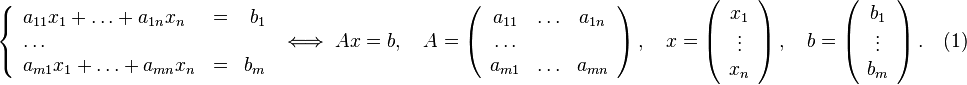
Матрица называется основной матрицей системы, — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
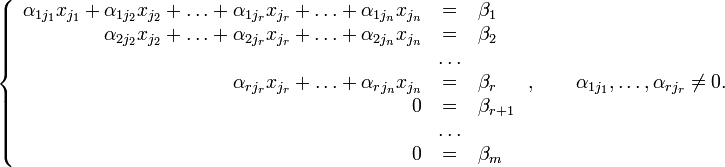
При
этом будем считать, что базисный
минор (ненулевой минор максимального
порядка) основной матрицы находится в
верхнем левом углу, то есть в него входят
только коэффициенты при переменных 
[3].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если
хотя бы одно число 
,
где 
,
то рассматриваемая система несовместна,
т.е. у неё нет ни одного решения.
Пусть 
для
любых
.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом
(
,
где 
—
номер строки):
,
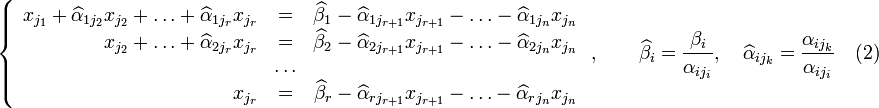где 
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
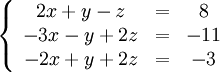
Обнулим
коэффициенты при
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на 
и 
,
соответственно:
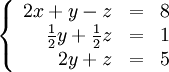
Теперь
обнулим коэффициент при 
в
третьей строке, вычтя из неё вторую
строку, умноженную на 
:
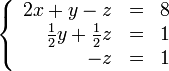
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
из
третьего;
из
второго, подставив полученное 
из
первого, подставив полученные
и
.
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
9-10. Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
A x + B y + C = 0
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
y = k x + b
где
k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках
x |
+ |
y |
= 1 |
a |
b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки A(x1, y1) и B(x2, y2), такие что x1 ≠ x2 и y1 ≠ y2 то уравнение прямойможно найти, используя следующую формулу
x - x1 |
= |
y- y1 |
x2 - x1 |
y2 - y1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
|
x = l t+ x0 |
y =m t+ y0 |
где (x0, y0) - координаты точки лежащей на прямой, {1, m}- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки A(x0, y0) лежащей на прямой и направляющего вектора n= {j; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
x - x0 |
= |
y- y0 |
j |
m |
Пример. Найти уравнение прямой проходящей через две точки A(1, 7) и B(2,3).
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x - 1 |
= |
y - 7 |
2 - 1 |
3 - 7 |
Из этого уравнения выразим y через x
x- 1 |
= |
y- 7 |
1 |
-4 |
y- 7 = -4(x- 1)y = -4x + 11
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2 то уравнение прямой можно найти используя следующую формулу
x- x1 |
= |
y - y1 |
= |
z - z1 |
x2 - x1 |
y2 - y1 |
z2 - z1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
|
x = j t+ x0 |
y = m t+ y0 |
|
z = n t+ z0 |
где (x0, y0, z0) - координаты точки лежащей на прямой, {j; m; n}- координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n= {j; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
x- x0 |
= |
y- y0 |
= |
z - z0 |
j |
m |
n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
|
A1x+ B1y+ C1z+ D1 = 0 |
A2x+ B2y+ C2z + D2 = 0 |
при условии, что не имеет место равенство
A1 |
= |
B1 |
= |
C1 |
. |
A2 |
B2 |
C2 |