
- •2. Матричные операции
- •3. Квадратная матрица и смежные определения
- •5. Системы линейных уравнений[править | править исходный текст]
- •Линейные преобразования[править | править исходный текст]
- •Описание метода
- •8. Метод Гаусса
- •11. Условие параллельности и перпендикулярности прямых
- •14. Эллипс
- •17. Понятие множества
- •18. Основные свойства функций.
- •19. Предел числовой последовательности
- •Сходящиеся и расходящиеся последовательности
- •Последовательность на бесконечности
- •21. Бесконечно малые и бесконечно большие величины.
- •Возрастание и убывание функции на интервале.
- •Точки экстремума
- •Теоремы о выпуклости функции и точках перегиба
- •36. Виды асимптот
- •38. Дифференциал функции
- •39. Применение дифференциала в приближенных вычислениях
- •40. Дифференциалы высших порядков
- •Случай независимой переменной
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.
Матрица
размера ![]() называется квадратной,число
называется квадратной,число ![]() называется порядком матрицы.
называется порядком матрицы.
Пример
![]() -
квадратная матрица порядка 2 или матрица
второго порядка.
-
квадратная матрица порядка 2 или матрица
второго порядка.
Определение
Матрица ![]() называется нулевой,
если все её
элементы равны
нулю, т.е.
называется нулевой,
если все её
элементы равны
нулю, т.е. ![]() .
.
Пример
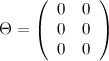
Определение
Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, - вектор-столбцом.
Пример
![]() -
вектор-строка;
-
вектор-строка; 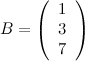 -
вектор-столбец.
-
вектор-столбец.
Диагональные матрицы
Определение
Квадратная
матрица ![]() называется диагональной,
если все ее элементы, стоящие вне главной
диагонали, равны нулю.
называется диагональной,
если все ее элементы, стоящие вне главной
диагонали, равны нулю.
Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.
Пример
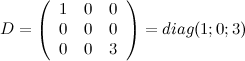
Определение
Скалярной называется
диагональная матрица ![]() ,
у которой все диагональные элементы
равны между собой.
,
у которой все диагональные элементы
равны между собой.
Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.
Пример
![]()
Определение
Единичной
матрицей ![]() называется
скалярная матрица порядка
, диагональные
элементы которой
равны 1.
называется
скалярная матрица порядка
, диагональные
элементы которой
равны 1.
Замечание. Для
сокращения записи порядок единичной
матрицы можно не писать, тогда единичная
матрица обозначается просто ![]() .
.
Пример
![]() -
единичная матрица второго порядка.
-
единичная матрица второго порядка.
2. Матричные операции
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая
матрица ![]() такая,
что её прибавление к другой матрице A
не изменяет A, то есть
такая,
что её прибавление к другой матрице A
не изменяет A, то есть
![]()
Все элементы нулевой матрицы равны нулю.
Возводить в степень можно только квадратные матрицы.
Ассоциативность сложения:
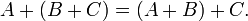
Коммутативность сложения:
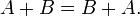
Ассоциативность умножения:
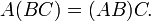
Вообще говоря, умножение матриц некоммутативно:
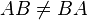 .
Используя это свойство,
вводят коммутатор матриц.
.
Используя это свойство,
вводят коммутатор матриц.Дистрибутивность умножения относительно сложения:
![]()
![]()
С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
Свойства операции транспонирования матриц:
![]()
![]()
![]() ,
если обратная
матрица
,
если обратная
матрица ![]() существует.
существует.
![]()
![]()
3. Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для
квадратных матриц существует единичная
матрица ![]() (аналог единицы для
операции умножения
чисел)
такая, что умножение любой матрицы на
неё не влияет на результат, а именно
(аналог единицы для
операции умножения
чисел)
такая, что умножение любой матрицы на
неё не влияет на результат, а именно
![]()
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
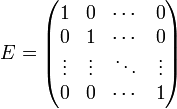
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица такова, что если матрицу умножить на обратную ей матрицу, то получится единичная матрица:
![]()
Обратная
матрица существует не всегда. Матрицы,
для которых обратная матрица существует,
называются невырожденными (или
регулярными), а для которых
нет — вырожденными(или сингулярными).
Матрица невырождена, если все ее строки
(столбцы) линейно
независимы как векторы.
Максимальное число линейно независимых
строк (столбцов) называется рангом
матрицы. Определителем (детерминантом)
матрицы называется значение
нормированной кососимметрической (антисимметрической) полилинейной
формы валентности ![]() на
столбцах матрицы. Квадратная матрица
над числовым полем вырождена тогда и
только тогда, когда ее определитель
равен нулю.
на
столбцах матрицы. Квадратная матрица
над числовым полем вырождена тогда и
только тогда, когда ее определитель
равен нулю.
4. Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы[
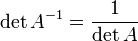 ,
где
,
где 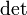 обозначает определитель.
обозначает определитель.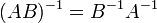 для
любых двух обратимых матриц
для
любых двух обратимых матриц 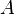 и
и 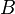 .
.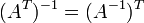 где
где 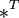 обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу.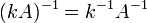 для
любого коэффициента
для
любого коэффициента 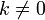 .
.Если необходимо решить систему линейных уравнений
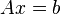 ,
(b — ненулевой вектор) где
,
(b — ненулевой вектор) где 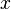 —
искомый вектор, и если
существует,
то
—
искомый вектор, и если
существует,
то 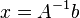 .
В противном случае либо
размерность пространства решений
больше нуля, либо их нет вовсе.
.
В противном случае либо
размерность пространства решений
больше нуля, либо их нет вовсе.
5. Системы линейных уравнений[править | править исходный текст]
Основная статья: Система линейных алгебраических уравнений
Рассмотрим систему линейных уравнений вида:
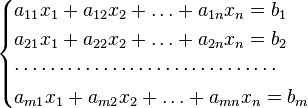 .
.
Эта
система состоит из ![]() линейных
уравнений относительно
линейных
уравнений относительно ![]() неизвестных,
может быть записана в виде следующего
матричного уравнения вида:
неизвестных,
может быть записана в виде следующего
матричного уравнения вида:
,
где
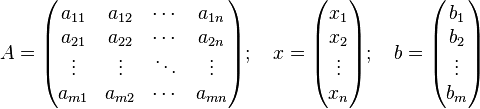
Матрица
—
это матрица коэффициентов системы
линейных уравнений, вектор-столбец
—
вектор неизвестных, а вектор-столбец ![]() —
некоторый заданный вектор.
—
некоторый заданный вектор.
Для того, чтобы система имела решение (хотя бы одно), необходимо и достаточно, чтобы вектор был линейной комбинацией столбцов , и тогда вектор — это вектор, содержащий коэффициенты разложения вектора по столбцам матрицы .
На языке матриц условие разрешимости системы линейных уравнений формулируется в виде теоремы Кронекера-Капелли:
ранг
матрицы
равен
рангу расширенной матрицы ![]() .
.
В
том случае, когда количество уравнений
совпадает с количеством неизвестных
(![]() ),
матрица
квадратная,
и условие разрешимости соответствующей
системы уравнений оказывается равносильным
условию невырожденности матрицы
.
),
матрица
квадратная,
и условие разрешимости соответствующей
системы уравнений оказывается равносильным
условию невырожденности матрицы
.
Тогда решение системы следует искать в виде
,
что очевидным образом приводит к алгоритму вычисления значений неизвестных переменных по правилу Крамера.
