26. Предельное критическое давление.

П редельное критическое давление это нагрузка, при которой зоны предельного равновесия сливаются в одну общую зону, отделяющую нагрузку от нижележащего массива грунта.

Предельное критическое давление является границей между фазами сдвигов и выпора.

В нормах на проектирование оснований принята форма огибающих зон предельного равновесия, предложенная Березанцевым(рис. 5.3, условно показана только левая часть симметричного графика). Решение сведено к трехчленному уравнению с протабулированными коэффициентами:

где Nγ , Nq, Nc– коэффициенты, функционально зависящие от угла внутреннего трения ϕ ; с– сцепление; b–ширина фундамента; q= γ ⋅h– пригруз.

В современной механике критические давления на грунт чаще всего определяются из решения смешанной задачи теории упругости и теории пластичности с использованием алгоритмов, реализуемых на ПЭВМ.

Достоинством таких решений является установление функциональных

зависимостей осадок от давлений в фазах сдвигов и выпора грунта. Замкнутые

аналитические решения, позволяющие получить такой результат, в нормах на проектирование оснований отсутствуют. По этой причине давления на

основания ограничивают величиной расчетного сопротивления грунта, а осадки рассчитывают с использованием линейной теории.

27. Давление грунта на подпорные стенки. Активное и пассивное давление грунта.

Ограждающие конструкции предназначены для удержания от обрушения находящийся за ним грунтовый массив. Характерным примером служит – подпорная стенка По конструктивному исполнению различают: 1)Массивные (гравитационные) – устойчивость обеспечивается собственным весом

2)Тонкостенные – собственным весом и весом грунта вовлеченным в работу, либо защемлением нижней части стенки в основание.

Эксперименты и натуральные наблюдения показывают, что равнодействующая давления грунта зависит от направления, величины и характера ее смещения

Если подпорная стенка под действием давления грунта не смещается и не изгибается то давление реализуется в условиях отсутствия горизонтального смещения при u=0, его часто называют давлением покоя E0.

Ординату горизонтального давления на вертикальную грань стенки определяют с использованием коэффициента бокового давления

Эпюра давления на боковую стенку при однородном грунте будет иметь вид треугольника и при высоте стенки h равнодействующая давления покоя определится как

Под действием давления грунта возможно так же смещение стенки в сторону от засыпки, принятое со знаком минус. Когда это значение достигнет величины -Ua , в грунте формируется область обрушения грунта, граница которой называется поверхностью скольжения, а сама область – призмой обрушения. Давление, передаваемое призмой – активным давлением Ea. Если подпорная стенка смещается в сторону грунта, в засыпке так же образуется поверхность скольжения, и при некоторой величине перемещения +Un, формируется призма выпирания. При этом реакция грунта достигает максимального значения и соответствует пас сивному давлению (отпору) грунта En28. Устойчивость подпорных стенок.

Р ассмотрим простейший случай, когда засыпка представлена идеально сыпучим грунтом. Поскольку принято что стенка имеет абсолютно гладкую грань, т.е. трение грунта о стенку отсутствует ( , вертикальная и горизонтальные площадки являются главными. Максимальное главное напряжение, действующее на горизонтальную площадку в точке контакта грунта со стенкой на глубине z от поверхности будет равно: . В переделах призмы обрушения ОАВ грунт находится в состоянии предельного равновесия, следовательно минимальное активное напряжение в точке 3 равно активному давлению и связано с максимальным главным напряжением условием предельного равновесия: (2) Подставив в уравнение высоту стенки h, получим максимальную ординату эпюры активного давления Равнодействующая активного давления Еа определяется как площадь эпюры а: 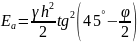. Из условия равновесия призмы плоскость скольжения АВ будет наклонена к вертикали под углом . Ширина призмы по поверхности засыпки l=htg(4 . При наличии на поверхности сплошной нагрузки: . .Если в пределах призмы обрушения приложена полосовая нагрузка шириной b: . Еа – площадь эпюры