12.) Отражение и преломление акустических волн на границах раздела сред. Трансформация волн. Критические углы.
Рассмотрим случай, когда плоская упругая волна, распространяясь в среде 1, падает под произвольным углом на границу раздела. Геометрия задачи и направление координатных осей показаны на рис.1.16. Волна частично проходит через границу, а частично отражается от нее. В отличие от анализа задачи с электромагнитными волнами для упругих волн необходимо принять во внимание не три, а пять волн: падающую, поперечную и продольную отраженные и поперечную и продольную преломленные. Если одна из сред является жидкостью или газом, поперечные волны в ней отсутствуют и общее число волн сокращается.
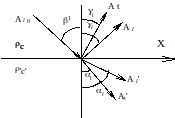
Рисунок 1.16 – Отражение и преломление волн на границе двух твердых сред.
В случае продольной падающей волны выполнение граничных условий эквивалентно следующему:
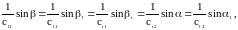(1.44)
где cl1, cl2, ct1, ct2 - скорости распространения продольных и поперечных волн в верхней и нижней средах . Отсюда вытекает
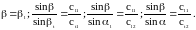(1.45)
Первое из этих соотношений есть закон равенства углов падения и отражения, а остальные являются обобщением закона Снеллиуса на случай упругих волн. Если падающая волна является поперечной, то условия на углы находятся аналогичным образом.
Дальнейшее решение задачи сводится к нахождению амплитуд отраженных и преломленных волн и коэффициентов отражения и прохождения.
Коэффициенты отражения R и прохождения D равны отношениям амплитуд соответствующих отраженных и прошедших и падающих волн, т.е.
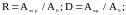(1.46)
где A0 - амплитуда падающей волны.
Коэффициент прохождения (отражения) по энергии выражается соотношением
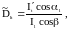(1.47)
где
-
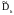коэффициент прохождения для поперечной
волны при падении продольной; Il
и
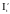- интенсивности падающей и преломленной
волн.
Коэффициенты отражения и прохождения по амплитуде
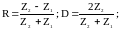
В случае, когда скорость распространения падающей волны меньше, чем скорость распространения какой-либо преломленной (или отраженной) волны, то существует критическое значение угла падения, при котором соответствующая преломленная (или отраженная) волна превращается в неоднородную волну, т.е. концентрируется вблизи границы и быстро затухает при увеличении расстояния.
Рассмотрим условия существования критических углов. Если первой и второй средой являются твердые тела, то из закона синусов вытекает возможность существования целого ряда критических углов.
Смотри ответ на вопрос номер 7!!!!!!!!!!!!!!!!!!
Рассмотрим пример падения продольной волны на границу двух твердых тел, разделенных тонким слоем жидкости: оргстекло - масло - сталь. На границу падает продольная волна, скорость которой cl1<ct2, поэтому имеются два критических угла (cl1=2670 м/с;ct2=3200 м/с). При этих углах все коэффициенты прохождения и коэффициент отражения Rlt обращаются в ноль, а коэффициент отражения Rll=1. В физическом смысле это означает смещение энергии вдоль поверхности неоднородной волной. На рис.1.18 приведены кривые изменения коэффициента прохождения в зависимости от угла падения продольной волны при различной толщине слоя жидкости.
В области углов (10...I) существуют одновременно волны двух типов. В связи с этим существенно затрудняется расшифровка результатов контроля, и поэтому данная область углов используется в дефектоскопии редко.
При первом критическом угле интенсивно возбуждается головная волна, которая применяется при НК.
В интервале между первым и вторым критическими углами существует только поперечная волна. Эта область углов (30...55) широко используется для возбуждения поперечных волн в дефектоскопии.
Аналогичный способ применяют для возбуждения поверхностных волн, волн в пластинах и стержнях. В этом случае угол преломления принимают равным 90, поэтому волны в ограниченных средах возбуждаются при угле падения
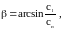(1.53)
где cп - скорость распространения поверхностной волны или фазовая скорость соответствующей моды волны в пластине или стержне.
В практике достаточно трудно получить плоскую волну, для которой выполняются приведенные выше графики и формулы. Вместо этого используют сферические волны, расходящиеся в пределах некоторого угла. При этом значения коэффициентов отражения и прохождения усредняют в некотором интервале углов падения.
При падении на поверхность раздела сред сферической волны отражение и преломление происходят так, как будто каждый из лучей является ограниченной плоской волной. При падении волны с углами несколько большими критического происходит интересное явление - незеркальное отражение. Установлено, что в этом случае отраженный пучок как бы смещается вдоль поверхности тела относительно падающего. Схематически это выглядит следующим образом (рисунок 1.19). При этом, чем ближе значение угла падения к критическому, тем больше смещение . Величина смещения определяется из выражения =2htg, где h - расстояние от действительной поверхности до мнимой границы отражения.
Данное явление можно рассматривать как перенос энергии вдоль поверхности неоднородной волной. Чем ближе угол падения к критическому, тем больше амплитуда неоднородной волны и тем большее расстояние она пробегает вдоль поверхности.