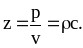7.) При каких условиях могут существовать критические углы на границе сред, в чём их смысл, как их определить, какие явления наблюдаются при этом?

Первый критический угол ^I при падении продольной волны существует при условии c_l1<c_l2. Он соответствует условию слияния продольной преломленной волны с поверхностью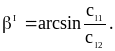 Распространяющаяся вдоль границы неоднородная волна, называемая головной, используется в дефектоскопии. Максимальное значение напряжения головная волна имеет под поверхностью объекта и с ее помощью удается обнаруживать подповерхностные дефекты.

Второй критический угол ^II существует при условии c_l1<c_t2 (падает продольная волна) и он соответствует условию слияния с поверхностью преломленной поперечной волны, т.е. В этом случае неоднородная волна подобна поверхностной рэлеевской волне и их трудно отличить друг от друга.

Третьим критическим углом называют угол падения поперечной волны, про котором отраженная продольная волна превращается в неоднородную. Он определяется выражением 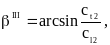при условии c_t2<c_l2.

При первом критическом угле интенсивно возбуждается головная волна, которая применяется при НК.

В интервале между первым и вторым критическими углами существует только поперечная волна. Эта область углов (30...55) широко используется для возбуждения поперечных волн в дефектоскопии.

Чем ближе угол падения к критическому, тем больше амплитуда неоднородной волны и тем большее расстояние она пробегает вдоль поверхности.

8.) Какими упругими постоянными характеризуются твёрдые среды? Что такое волновое сопротивление среды и чем оно определяется?

Как уже отмечалось ранее, упругие свойства твердых тел характеризуются двумя независимыми упругими постоянными. При этом в качестве пары упругих констант могут быть использованы скорости продольных и поперечных волн в безграничной среде. Через их значения можно определить скорости распространения других типов волн и константы упругости cреды (E, G, ).Для акустического контроля важное значение имеет такая характеристика cреды как акустический импеданс (комплексное сопротивление). Этот параметр определяется отношением акустического давления к колебательной скорости в упругой волне. В случае рассмотрения безграничной cреды, где потери УЗ- энергии несущественны, акустический импеданс является действительной величиной и определяется выражением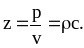 . Скорость продольной волны в твердом теле: 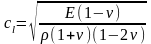, E-модуль нормальной упругости. Скорость поперечной волны: , G-модуль сдвига.

В твердых телах, характеризующихся двумя упругими постоянными: коэффициентом сжимаемости — деформацией сжатия (растяжения) и упругостью формы (деформацией сдвига или изгиба), могут возникать, кроме продольных волн, еще и поперечные волны сдвига, изгиба и т. п. При этом у продольных волн направление колебаний частиц среды совпадает с направлением распространения звуковых волн, а у поперечных волн — перпендикулярно этому направлению.

Величину z называют характеристическим импедансом или волновым сопротивлением cреды, и она определяет условия отражения и преломления волн на ее границе. При нормальном падении плоской волны на плоскую границу раздела двух сред коэффициент отражения определяется только отношением волновых сопротивлений этих сред.