
- •1 Модуль
- •1.) Назовите основные величины, характеризующие акуст. Волны и поясните их физический смысл и взаимосвязь.
- •2.) Физический смысл тензора деформаций и тензора напряжений. З-н Гука, его физический смысл.
- •3.) Дайте понятие интенсивности и энергии звуковой волны. В чём отличие волновых уравнений для описания бегущих и стоячих волн?
- •4.) Какие типы волн могут распространяться в газовых, жидкостных и твёрдых средах? Какими физическими величинами определяются скорости распространения упругих волн?
- •5.) Какие виды поверхностных волн могут распространяться на границах раздела сред и в чём их особенность? Опишите возможные способы возбуждения поверхностных волн.
- •6.) В чём особенность нормальных волн и в каких условиях они могут существовать? Физический смысл дисперсии скорости звука. Практические способы возбуждения нормальных волн.
- •7.) При каких условиях могут существовать критические углы на границе сред, в чём их смысл, как их определить, какие явления наблюдаются при этом?
- •8.) Какими упругими постоянными характеризуются твёрдые среды? Что такое волновое сопротивление среды и чем оно определяется?
- •9.) Назовите основные акустические характеристики сред. Поясните механизм затухания акустических волн.
- •10.) Как зависит коэффициент затухания от структуры среды и от частоты колебаний? Какое значение придаётся затуханию волн в акустическом контроле?
- •11.) Механизм затухания волн в различных средах. Поглощение и рассеяние волн.
- •12.) Отражение и преломление акустических волн на границах раздела сред. Трансформация волн. Критические углы.
- •Коэффициенты отражения и прохождения по амплитуде
- •13.) В чём сущность з-а Снеллиуса при падении акустической волны на границу раздела 2-х сред? в чём сущность коэффициентов отражения и прохождения и от чего они зависят?
- •14.) Как используется наличие критических углов в практике контроля?
- •15.) Как определить угол падения акустических волн при заданном угле ввода пучка в обьект?
- •16.) Особенности отражения волн от свободной границы твёрдого тела. Обменные углы.
- •17.) Дифракция волн в твёрдых телах. Явление поляризации для акустических волн.
- •18.) Отражение и прохождение акустических волн при нормальном падении на границу двух сред, разделенных тонким слоем. Просветление границы.
1 Модуль
1.) Назовите основные величины, характеризующие акуст. Волны и поясните их физический смысл и взаимосвязь.
Акустические колебания - это механические колебания частиц упругой среды, а волны - распространение в этой среде механического возмущения. В жидкостях и газах акустические волны характеризуются одной из следующих величин:
а) акустическим давлением р (изменением давления);
б) смещением u частиц среды из положения равновесия;
в) скоростью колебательного движения частиц среды v;
г) потенциалом смещения или колебательной скорости .
Взаимосвязь перечисленных величин определяется зависимостями
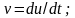 (1.1)
(1.1)
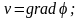 (1.2)
(1.2)
 (1.3)
(1.3)
где - плотность среды; t - время.
2.) Физический смысл тензора деформаций и тензора напряжений. З-н Гука, его физический смысл.
В
общем случае, когда присутствуют все
виды деформации, состояние тела
определяется заданием в каждой точке
девяти чисел. Они образуют компоненты
тензора деформации. Поскольку этот
тензор симметричен, то различных чисел
здесь только шесть. В общем виде элемент
тензора удобно записать в виде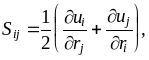 где i,
j
- x,
y,
z.Тензор
деформации является безразмерной
величиной. Численные значения Sij
для различных материалов изменяются в
широких пределах. Например, для резины
реально достижимы значения порядка
единиц, а для более жестких материалов
значение Sij
достигает 10-4
и ограничивается остаточной деформацией
или разрушением.Тензор второго ранга,
называется тензором напряжений и имеет
размерность Н/м2.
где i,
j
- x,
y,
z.Тензор
деформации является безразмерной
величиной. Численные значения Sij
для различных материалов изменяются в
широких пределах. Например, для резины
реально достижимы значения порядка
единиц, а для более жестких материалов
значение Sij
достигает 10-4
и ограничивается остаточной деформацией
или разрушением.Тензор второго ранга,
называется тензором напряжений и имеет
размерность Н/м2.

Такой тензор называют симметричным. В жидкостях и газах тангенциальные компоненты отсутствуют, а нормальные равны между собой. Давление считается положительным, когда оно сжимающее, и отрицательным, когда растягивающее (напряжение в этом случае положительное).
Согласно закону Гука для изотропного тела можно записать уравнения, связывающие компоненты тензоров Tij и Sij
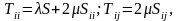 (1.6)
(1.6)
где S=Sxx+Syy+Szz - изменение единицы объема;
и - упругие постоянные или компоненты Ламе.
Выражение (1.6) называется обобщенной формой закона Гука. Вместо постоянных и можно использовать модуль упругости E и модуль сдвига G или E и коэффициент Пуассона .
Время Т, в течение которого совершается один полный цикл колебания в УЗ волне, называют периодом колебаний.
Количество колебаний, происходящих за 1 секунду, называют частотой f колебаний в УЗ волне.
Максимальное значение, которое принимает переменный параметр за период (смещение U или скорость V), называют амплитудой.
Фазой УЗ волны называют параметр, показывающий, какая часть периода прошла с момента начала последнего цикла колебания. Если нам известна фаза УЗ колебания, это значит, что мы знаем, каковы смещение и скорость колеблющейся частицы, а также в каком направлении движется частица в данный момент времени.
Длиной
УЗ волны X называется минимальное
расстояние между двумя точками,
колеблющимися в одной фазе. Длина волны
связана с частотой и скоростью соотношением
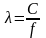 .
.
