30 Вопрос.

Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами   и   называется количество отличных бит на соответствующих позициях, то есть число «единиц» в векторе  .

Минимальное расстояние   линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов.

Вес вектора —   расстояние Хемминга между этим вектором и нулевым вектором, иными словами — число ненулевых компонент вектора.

Теорема 1:

Минимальное расстояние   линейного кода равно минимальному из весов Хемминга ненулевых кодовых слов:

Доказательство:

Расстояние между двумя векторами   удовлетворяет равенству  , где   — вес Хемминга вектора  . Из того, что разность любых двух кодовых слов линейного кода также является кодовым словом линейного кода, вытекает утверждение теоремы: 

Минимальное расстояние Хемминга   является важной характеристикой линейного блокового кода. Она определяет другую, не менее важную характеристику — корректирующую способность:

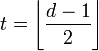, здесь угловые скобки обозначают округление «вниз».

Корректирующая способность определяет, какое максимальное число ошибок в одном кодовом слове код может гарантированно исправить.

Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем B. Но если каналом были внесены ошибки в двух битах, декодер может посчитать, что было передано слово B.

Число обнаруживаемых ошибок — число ошибок, при котором код может судить об ошибочной ситуации. Это число равно

.

Теорема 2 (без доказательства):

Если любые   столбцов проверочной матрицы H линейного (n, k)-кода линейно независимы, то минимальное расстояние кода равно по меньшей мере d. Если при этом найдутся d линейно зависимых столбцов, то минимальное расстояние кода равно d в точности.

Теорема 3 (без доказательства):

Если минимальное расстояние линейного (n, k)-кода равно d, то любые   столбцов проверочной матрицы H линейно независимы и найдутся d линейно зависимых столбцов.

31 Вопрос.

Эта таблица нарисована в тетради.

32 Вопрос.

Пре́фиксный код в теории кодирования — код со словом переменной длины, имеющий такое свойство (выполнение условия Фано): если в код входит слово a, то для любой непустой строки b слова ab в коде не существует. Хотя префиксный код состоит из слов разной длины, эти слова можно записывать без разделительного символа.

Например, код, состоящий из слов 0, 10 и 11, является префиксным, и сообщение 01001101110 можно разбить на слова единственным образом:

0 10 0 11 0 11 10

Код, состоящий из слов 0, 10, 11 и 100, префиксным не является, и то же сообщение можно трактовать несколькими способами.

0 10 0 11 0 11 10

0 100 11 0 11 10

Определение

Так называемые «префиксы» могут быть получены путём последовательного отбрасывания последнего знака кодовой комбинации. Например, для кодовой комбинации 11101101 префиксами будут 11101101, 1110110, 111011, 11101, 1110, 111, 11, 1.

Если промежутков или других знаков препинания между кодовыми комбинациями нет, то для однозначного декодирования комбинации 111011101 ни одна из кодовых комбинаций не может быть представлена перечисленными вариантами (префиксами). Код называется префиксным, если ни одна из его комбинаций не является префиксом другой комбинации того же кода. Часть кодовой комбинации, которая дополняет префикс до самой комбинации, называется суффиксом. Префиксные коды наглядно могут быть представлены с помощью кодовых деревьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода.