5.2.3. Расчёт элементов, работающих на изгиб

В случаях, когда при нагружении пружина должна иметь небольшой прогиб, используются прямые и изогнутые пружины, работающие на изгиб. Обычно они имеют прямоугольное сечение, реже круглое. Применяются в электрических контактных устройствах (реле), в качестве рессор для растяжек и подвесов точных приборов, а также в случаях, когда требуется получить большой прогиб и пологую характеристику чувствительного элемента.

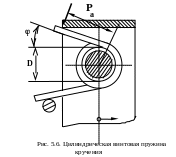
Цилиндрические винтовые пружины кручения (рис.5.6) приме­няются для создания крутящего момента М при закручи­вании свободного конца пружины на угол . Материал таких пружин в основном испытывает напря­жения изгиба, поэтому диаметр про­во­локи оп­ре­де­ляется из условия прочности на изгиб

3

d   P a/(0,1 [) ,

где [- допускаемые изгибные напря­жения. Принимается ближай­шее по сор­та­менту значение d (по ГОСТу) и определяется диаметр пружины D =(512) d.

Спиральные пружины применяются в часовых механизмах, самопи­шу­щих, измерительных и других приборах в качестве пружинных двигателей (завод­ные пружины), для создания притиво­дейст­вующего момента, подвода тока к подвижным рамкам электро­из­мерительных приборов (моментные пружины).

Для изготовления спиральной пружины тонкая метал­лическая лента плотно (виток к витку) навивается на цилиндрическую оправку и в таком состоянии выдерживается от 2 до 10 дней. В результате такого заневоливания пружины, в ней возникают остаточные дефор­мации изгиба и она приобретает спиралеобразную форму.

Внутренний конец пружины прикрепляется к валику, а наружный - к корпусу механизма. При вращении валика пружина закручивается, радиус кривизны витков уменьшается и в её материале возникают напряжения изгиба, создающие пропорциональный углу закру­чивания противодейст­вую­щий момент.

Задачей расчёта пружины является определение основных её размеров (толщины, ширины и длины ленты или диаметра прово­локи) по заданным противодействующему моменту и рабо­чему числу оборотов барабана или углу закручивания пружины.

Задача. Для балки c заданной расчётной схемой (рис. 5.7) требуется напи­­сать выражение поперечных сил Q, изгибающих моментов М_И и прогибов w для каждого участка в общем виде, построить эпюры Q, М_И и w, найти М_мах и подобрать стальную балку двутаврового поперечного сечения при [] =160 МПа.

Дано: m=40 кН м, F=20 кН; q = 100 кН/ м.

Вид нагружения бруса в данной задаче - простой изгиб, при котором в поперечном сечении возникают поперечные силы и изгибающие моменты.

А

В

q m F

Рис.5.7. Расчётная схема балки

1. Решение задачи следует начинать с определения реакций опор. Пред­ставим балку как свободное тело, для чего отбросим опоры А и В, а их действие на балку заменим реакциями R_A и R_B.

Опора А- шарнирно-неподвижная. Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. При решении задачи реакцию опоры изобра­жают её проекциями: Z_A на ось z балки и Y_А на ось у, пер­пендикулярную оси балки (рис.5.8 а). Опора В - шарнирно-подвиж­ная. Реакция такой опоры R_B направлена по нормали к опорной поверхности, в данном случае перпендикулярно оси балки.

Таким образом, имеем три неизвестных: Z_A, Y_A, Y_B, для опре­деления которых необходимо составить три уравнения равновесия :

 M_A = 0 ;  M_B = 0 ; Z = 0 .

Последнее уравнение необходимо для определения реакции Z_A, которая в нашем случае равна нулю.

Уравнение суммы моментов относительно опоры В позволяет определить реакцию Y_А

 М_B = Y_A ·6 - q ·3 · 4,5 + m + F· 2 = 0 ;

У q = 100 кН/м m=40 кН м F=20 кН

а) Z_A=0

z

z₁ I II III IV

Y_A= z₂ Y_B=108 кН

=212 кН z₃

z₄

3 м 1 м 2 м 2 м

б)

Q, кН

z_1Э

в)

М_И, кН м

г )

Рис. 5.8. Расчётная схема (а), эпюры поперечных сил Q (б),

изгибающих моментов М_И (в) и изогнутая ось балки (г).

Y_A = (100· 3· 4,5 - 40 - 20 ·2)/6  212 (кН) .

Реакцию Y_B определим по условию равенства нулю суммы моментов относительно опоры А :

 M_A = q· 3 ·1,5 + m - Y_B ·6 + F ·8 = 0 ;

Y_B = (100 ·3 ·1,5 + 40 + 20 ·8)/6  108 (кН).

Проверка. Правильность нахождения реакций опор можно оценить, составив, например, уравнение суммы проекций всех сил на ось Y

 Y = Y_A - q·3 + Y_B - F = 212 - 100·3 + 108 - 20 = 0 ,

реакции найдены верно.

2. Построение эпюр Q и М_И. Разбиваем балку на участки. За гра­ни­цы участков принимаем сечения, в которых приложены мо­мент m, сила F, либо нахо­дится граница действия распределённой нагрузки q. В данном случае имеем четыре участка: I, II, II и IV (рис. 5.8, а). Выбираем начало координат в точке (опоре) А и приступаем к построению эпюр поперечных сил Q и изгибающих моментов МИ, применяя метод сечений.

Проводим сечение в пределах участка I (0  z ₁  3 м ) на расстоянии z₁ от начала координат. Мысленно отбра­сы­ва­ем правую часть балки и рассматриваем равновесие оставшейся ле­вой части. Согласно сфор­мулированным принципам расчёта, воз­ни­ка­ющая в сечении попереч­ная сила численно равна алгебра­­ической сум­ме проекций на вертикальную ось всех действующих на рас­смат­риваемую часть внешних сил, а изги­ба­ющий момент – алгеб­раи­ческой сумме моментов всех сил, действующих на рас­смат­риваемую часть, относительно проведённого сечения. Таким образом :

Q I= Y_A - qz₁ = 212 - 100·z₁ ;

M_ИI = Y_A z₁ - q z²₁/2 = 212·z₁ - 50· z²₁ .

Функция Q_I = f(z₁) описывается уравнением первого порядка (наклонная прямая), функция М_И1=f(z₁)- уравнением второго поряд­ка (парабола) относи­тельно переменной координаты сечения z₁. При этом очевидно выполнение теоремы Журавского: первая про­из­водная от изгибающего мо­мен­та по абсциссе z сечения равна поперечной силе. Задавая значения z₁, соответ­ствующие границам участка I, получим:

Q_I (z₁= 0) = 212 кН ; М_I (z₁=0) = 0 ;

Q_I (z₁=3 м) = 212 - 100·3 = -88 (кН);

M_I (z₁=3 м) = 212·3 - 50· 3² = 186 (кН м).

Строим эпюры для первого участка и отмечаем на них полученные значения Q_I и M_ИI (рис.5.8)

Эпюра моментов, расположенная под распределённой нагруз­кой (учас­ток 1), может иметь в пределах участка экстремальное значение. Признаком экстремума является условие dM_И/dz=0, или сме­на знака поперечной силой Q, наглядно изобра­жае­мая пересе­че­нием графика Q(z) и нулевой линии на эпюре.

Для нахождения экстремального значения изгибающего момен­та на участ­ке I решим уравнение dM_И(z₁)/dz=0 или Q(z₁) = 0 относительно z₁, а за­тем при найденном корне z_1Э одного из этих уравнений определим величину М_И:

dM_ИI/dz₁=Y_A - qz_1Э= 212 - 100· z_1Э =0,

откуда

z_1Э = 212/100=2,12 (м).

Подставив значение z_1Э = 2,12 м в уравнение моментов для участка I, найдём величину экстремального момента :

M_ИImax=Y_A z_1Э - q z_1Э² /2 =212· 2,12 -50 ·2,12² = 225 (кН м).

Выражения поперечных сил и изгибающих моментов на участке II (3 м < z₂  4 м)выглядят следующим образом:

Q_II = Y_A - q ·3 = 88 (кН) ,

М_ИII = Y_А z_II - q 3 (z₂ - 1,5) .

При z₂ = 3 м М_ИII= 212·3 - 100·3·1,5 = 186 (кН м).

При z₂ = 4 м М_ИII = 212·4 - 100 ·3·2,5 = 97 (кН м).

Для участка III (4 м < z₃  6 м) получим

Q_III= 212 – 100·3 = - 88 (кН) ,

М_ИIII= Y_A z₃ - q·3 (z₃ - 1,5) + m .

При z₃= 4 м М_ИIII =212·4 - 100·3·2,5 + 40 = 137 (кН м) .

При z₃ = 6 м M_ИIII = 212·6 - 100·3·4,5 + 40 = - 40 (кН м).

Для участка IV (6 м < z₄  8 м)

Q_IV = Y_A - q·3 + Y_B = 212 - 100·3 + 108 = 20 (кН) ,

М_ИIV = Y_A ·z₄ - q ·3 (z₄ - 1,5) + m + Y_B (z₄ - 6) .

При z₄ = 6 м М_ИIV = 212·6 - 100·3·4,5 + 40 + 0 = - 40 (кН м).

При z₄ = 8 м М_ИIV = 212·8 - 100·3 ·6,5 + 40 + 108·2 = 0.

3. Для проверки правильности построения эпюр Q и М_И удобно поль­зоваться теоремой Журавского: dM_И /dz = Q.

Из курса высшей математики известен геометрический смысл первой про­из­­водной от какой-либо функции: она равна тангенсу угла наклона, образованному между ка­са­тельной к графику этой функции и положи­тель­ным направлением оси аргу­мен­та. Если первая производная, а следова­тельно, и указанный угол наклона положительны, то значения функции возрастают при возрастании значений аргумента, а если отрицательны - то убывают. При равенст­ве первой про­из­водной нулю, функция имеет экстре­мум - максимум или минимум.

Описанная связь между функцией и её производной исполь­зуется при проверке правильности построенных эпюр поперечных сил и изгибающих моментов.

4. Для подбора сечения балки используют условие прочности. Номер балки определяется по моменту сопротивления её сечения, рассчитываемому по формуле

W_X  M_{И MAX} / [] ,

где М_{И МАХ} - максимальное значение изгибающего момента, действу­ющего по длине балки, определяется по эпюре изгибающих момен­тов. В нашем случае М_{И МАХ} = 225·10³ Нм (рис. 5.8), []=160·10⁶ Па ,

W_X  225·10³ / (160·10⁶ )= 1,406 10 ^-3 (м3 )= 1406 (см³ ).

В соответствии с результатами этого расчёта по таблице сортамента выбираем двутавр № 50, W_X=1589 cм³ , I_X=39727 cм⁴.

5. Определение прогибов в рассматриваемой балке методом непос­редст­вен­ного интегрирования дифференциального уравнения её изогнутой оси сопряжено со значительными расчётными труд­нос­тями, связанными с определением произвольных посто­ян­ных интегрирования. Поэтому для решения задачи пользуются разли­чными расчётными методами. Наиболее часто используются расчёты, осно­ван­ные на использовании интеграла Мора, правила Вереща­гина, однако при их реализации требуется введение допол­ни­тельных понятий, не имеющих четкого физического смысла. Методоло­гичес­ки же более удачным, на наш взгляд, является метод нача­льных параметров, который основан на следующих исходных поло­жениях.

а) Начало координат, в которых задаётся расположение сече­ния балки, выбирают в крайней левой точке рассматриваемой части балки, и оно является общим для всех участков. Это положение использовано раньше, но, в отличие от расчётов М_И и Q, при использовании входящих в дифференциальное уравнение изогнутой оси выражений М_И(z), оно является обязательным.

б) Выражение для изгибающего момента М_И(z) составляется путём вы­чис­­ления моментов сил, расположенных слева от рассматриваемого сечения, взятого на расстоянии z от начала координат.

в) При включении в уравнения изгибающего момента внешнего сосре­до­то­ченного момента m, приложенного на некото­ром расстоянии z_m от начала координат, его умножают на множи­тель (z - z_m)⁰, равный единице.

г) В случае обрыва распределённой нагрузки (в рас­сматриваемом случае в сечении с координатой z=3м) её продлевают до конца рассматриваемого участка (рис.5.8 а), а для восстановления фактически действующего на балку воздействия вводят компен­сирующую нагрузку обратного направления (экстра­­по­лированную дополнительную нагрузку и нагрузку её компенси­рующую, принято показывать штрихами).

д) Интегрирование уравнений на всех участках производят без раскры­тия скобок.

При таком подходе выражение изгибающего момента на любом участке балки будет представлено через внутренние силовые факторы и внешние нагрузки, действующие слева от рассматри­ва­емого сечения, включая изгибающий момент М₀ и поперечную силу Q₀, действующие в сечении, совпадающем с началом координат. Величины М₀ и Q₀, так же как и прогиб w₀ и угол поворота ₀ сечений балки в начале координат, называются начальными пара­мет­рами. В частности, изгибающий момент в сечениях четвёртого участка балки будет

М_ИIV (z₄)= М₀ + Q₀·z₄ - q(z₄-0)²/2 + q(z­₄-3)²/2 + m (z₄ - 4)⁰ +Y_B(z₄-6),

где М₀=0, Q₀=Y_A , поскольку начало координат совпадает с опорой А. После подстановки изгибающего момента в дифференциальное уравне­ние изогнутой оси балки, двукратного его интегрирования и определения постоянных интегрирования, которыми оказываются начальные параметры

С₁ = ₀ и С₂= w₀,

получаем следующие уравнения зависимости угла поворота и прогиба сечения балки

(z₄) = ₀ + [М₀z₄+ Q₀ z₄²/2 - q(z₄-0)³/6 + q(z­₄-3)³/6 + m(z₄ - 4) +Y_B(z₄-6)²/2]/(EI_x)

w(z₄) = w₀+₀z₄+ [М₀z₄²/2+ Q₀z₄³/6 - q(z₄-0)⁴/24 + q(z_­4-3)⁴/24 +

+m (z₄ - 4)²/2 + Y_B(z₄-6)³/6]/(EI_x).

Геометрические начальные параметры ₀ и w₀ определяются из условий деформирования на опорах. В данном случае для их определения исполь­зуются уравнения w(z₁=0)=0 и w(z₄=6)=0, из которых получаем

w₀=0 ,

₀= - [М₀6²/2+ Q₀6³/6 - q(6-0)⁴/24 + q(6-3)⁴/24 + m (6 - 4)²/2 +

+ Y_B(6-6)³/6]/(6EI_x)= - [0+212·6³/6 -100·(6-0)⁴/24 +100 (6-3)⁴/24+ + 40 (6 - 4)²/2 + 108(6-6)³/6]/(6· 2·10⁸ ·39,727 ·10 ^-5) = - 5,56 10-3 ,рад.

Рассчитав прогибы и углы поворота в различных сечениях балки, строим её изогнутую ось (рис. 5.8 г). Для проверки правиль­ности построения следует использовать дифференциальную связь между углом поворота сечения балки и изгибающим моментом (по аналогии использования теоремы Журавского)

d/dz=M(z)/EIx)

Контролирующей здесь также является ориентация выпук­лос­ти изогнутой оси балки, которая направлена вниз при положительном изгибающем моменте, и вверх- при отрицательном.

Биметаллические пружины деформируются при изменении темпера­туры. Они изготавливаются из двух спаянных, сваренных или совместно про­катанных тонких металлических пластин с толщинами h₁ и h₂, материалы которых должны иметь близкие значения модулей упругости Е₁ и Е₂ и допускаемых напряжений на изгиб, наибольшую разность между значе­ниями коэффициентов температурного линейного расширения ₁ и ₂, хорошую свари­ваемость. В качестве слоя с малым температурным расширением чаще всего применяется инвар ЭН-36 (ферромагнитный сплав железа с 36 % никеля ₂= 1,5 10^-6 1/⁰C), а с большим - латунь или немагнитная сталь (₁= 13…17,5 10^-6 1/⁰C).

На рис.5.9 показаны примеры конструкций биметаллических пружин. При нагревании пружина изгибается в сторону пластины с меньшим коэффици­ентом линейного расширения.

Для получения наибольшей чувствительности биметал­личес­кой пружины к изменению температуры необходимо соблюдать условие

h ₁/h₂=  Е₂/Е₁

При изменении температуры от t₁ до t₂ наибольший прогиб f свободного конца прямой пружины, закреплённой одним концом как консоль (рис. 5.9, а) определяется по формуле

f=0,75 (₁- ­₂) l ² (t₁-t₂)/(h₁+h₂)

Сила Р, которая создаётся биметаллической пружиной, нажимающей на упор А , находится по формуле

Р = (Е₁ + Е₂) bh³ (f - f_уп) / (8 l ³),

где h=h₁ + h₂ ; f - прогиб свободной пружины; f_уп - прогиб пружины при наличии упора; l - длина пружины.

В случаях, когда биметаллические пружины нагреваются током, проходящим непосредственно через них или через обмотку, для устранения ошибок, возникающих от колебаний температуры среды, в конструкцию устройства термочувствительного элемента вводится вторая биметал­ли­чес­кая пружина, которая компенсирует прогиб основной пружины или компенсирует усилие.

а)

Биметаллические пружины надёжны в работе, имеют простую конструк­цию и малую стоимость. Они применяются в приборах в качестве изме­ри­тельных, движущих и регулирующих элементов тер­мо­регуляторов, термо­компенсаторов, температурных реле, автома­тических предохранителей, тер­мо­графов, термометров, электроиз­мерительных приборов (вольтметров и ам­пер­метров). На рис. 5.9, б приведена схема термометра с плоской пласти­ной.

Сильфоном называется тонко­стенная цилиндрическая труб­ка, стен­ки которой имеют глубокие волнооб­разные склад­ки (гофры, рис. 5.10). Под действием внут­реннего или внешнего давления газа или жидкости, а также сил, при­ложен­ных к крайним сечениям сильфона, его стенки деформируются. При этом изме­няется длина и внутрен­ний объём силь­фона, а иногда и распо­ложение его оси (при изгибе). Все основ­­ные па­­раметры, конст­рукция и раз­меры прибор­ных бес­шов­ных одно­с­лой­ных сильфонов стандарти­зированы.

В ГОСТах для каждого типоразмера сильфона приведены величины эф­фек­тивной площади F_эф=F_н-F_в, жёсткости по сосредо­то­чен­ной силе Q, наи­больший ход, соответствующий наибольшему давлению жидкости или газа.

Рис.5.10. Сильфон и его основные параметры

Мембраны представляют собой тонкую круглую плоскую, выпуклую или гофрированную пластинку, заделанную (слегка зажа­тую) или жёстко закреплённую (пайкой или сваркой) по конту­ру. Под действием осевой сосредоточенной силы или силы давления р газа или жидкости мембрана прогибается. Применяются плоские, хлопающие (в форме сферического купола) и гофриро­ванные метал­лические мембраны.

Для повышения чувствительности (увеличения суммарного прогиба) упругого элемента прибора из двух мембран путём сварки или пайки изготовляют гофрированные мембранные коробки (рис.5.11). Существуют:

- манометрические коробки, внут­рен­­няя полость которых сое­ди­няется с кон­т­ролируемой сре­дой с изменя­ю­щим­­ся давлением (применяют в маномет­рах, ва­риометрах, указателях ско­рос­ти и других приборах);

-

р

анероидные коробки, из внут­рен­ней полости которых вы­ка­чан воздух (до 0,1 мм рт. ст.), слу­жат для изме­ре­ния абсолют­ного давления, применя­ются в вы­сото­мерах и вакуумметрах;

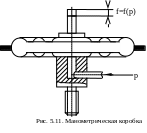
- наполненные коробки, внутренняя область которых запол­нена газом (азотом) или насыщенными парами эфира (применяются в некоторых типах терморегуляторов и термометров.

В приборах часто применяются групповые блоки, собранные из нескольких мембранных коробок. Характеристика мембраны зависит от её материала, размера и профиля гофров. Материалом для мембран служат: нержавеющие стали, бронзы, резина, прорези­ненный шёлк и кожа, а конструкция, основные параметры и размеры измерительных гофрированных мембран стандартизи­рова­ны. Про­фили мембран бывают трапецеи­дальными, угловыми, сину­со­и­даль­ными с постоянной и переменной глубиной. Выбор мембран про­изводится по требуемому значению давления и соответству­ю­щему ему перемещению центра мембраны.

Трубчатые манометрические пружины (трубки Бурдона) представляют со­бой тонкос­тен­ные металлические трубки эллипти­ческого или овального вы­тя­нутого сечения (рис.5.12), изогнутые по дуге окружности, по винтовой ли­нии или по спирали. Один конец трубки должен быть запаян наглухо, а вто­рой припаян к держателю (штуцеру). Через держатель во внутреннюю по­лость трубки подаётся газ или жидкость. При повышении внутреннего дав­ления вследствие упругой деформации стенок радиус кривизны трубки уве­личивается и запаянный её конец перемещается тем больше, чем больше раз­ность давлений внутри и вне трубки. Материалом для



1

2

2а

2b

2b

h

2а

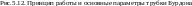
изготовления труб­­­чатых пружин служат латунь, фосфористая бронза, бериллиевая брон­за.

Ч увствительностью трубчатой пру­жи­ны называется величина отно­шения перемещения её конца к единице изменения давления. Поскольку она существенно ниже чувствительности сильфонов и мембранных коробок, трубчатые пружины применяют для измерения больших давлений от 0,05 до 40 МПа. В приборах с трубками, изогнутыми по дуге окружности 270 , для передачи движения от конца трубки к указателю 1 манометра применяются множительные передаточные механизмы.

Для того чтобы на стрелку 1 при­бо­ра передать полное переме­щение f кон­ца пружины, тягу 2 переда­точного меха­низ­ма следует распо­лагать по нап­равлению этого пере­ме­щения.

При проектировании трубчатой пру­жины необходимо выби­рать опти­маль­ные размеры трубки (а/b= 56, , h), при которых труб­ка обладала бы вы­соким пределом пропорциональнос­ти и дос­таточной чувствитель­ностью. Реко­мен­дуется принимать стан­дарт­ные зна­чения размеров.

П

А

F

F_g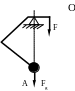

римером неупругих меха­ни­ческих чувствительных элементов яв­ля­ется ры­чаж­ный чувствительный элемент, пе­ре­мещение одной из точек (точки А, рис. 5.13) рычага кото­рого связано с вели­чиной F изме­ряемого усилия, момент от кото­рого уравно­веши­вается силами тя­жес­ти F_g звеньев механизма. Принципы работы других механических чувствительных элемен­тов показаны на рис. 5.14,5.15

Рис. 5.13. Схема рычажного

чувствительного элемента