5.2.2. Расчёт элементов, работающих на кручение

Задача. К стальному ступенчатому валу, имеющему сплошное попе­реч­ное сечение, приложены четыре момента (рис. 5.4) Левый конец вала жёстко закреплён в опоре, а правый - свободен. Требуется: 1. Построить эпюру крутящих моментов по длине вала.

2. При заданном значении допускаемого напряжения на кручение опре­делить диаметры d1 и d2 вала из расчёта на прочность, полученные значения округлить.

3. Построить эпюру максимальных напряжений кручения по длине вала.

4. Построить эпюру углов закручивания, приняв G = 8·104 МПа.

Дано: a=1,0 м, b=1,0 м , c=1,0 м , T1=5,1 кН м, Т2= 2,1 кН м, Т3=1,1 кН м, Т4= 0,1 кН м, []=50 МПа.

Р

b

ЕШЕНИЕ. В данном случае брус подвержен круче­нию, т. е. такому виду нагружения, при котором в поперечных сечениях бруса возникают только крутящие моменты. Этот момент опреде­ляется по внешним скручивающим моментам с по­мощью метода сечений (см. преды­дущую задачу). На основании этого мето­да мож­но показать, что крутящий момент, воз­ни­кающий в произ­вольно выб­ран­­ном попереч­ном сечении бруса, оп­ре­де­ляется как алгебра­ическая сум­­ма внешних скручивающих мо­мен­тов, прило­жен­ных к брусу по од­ну сторону от рассматриваемого сечения. Наиболее удобно крутящие

T₁ T₂ T₃ T₄

а)

б)

в)

г)

d₁

d₂

IV III II I

а b с d

М_К, кНм

1,1

0,1

1,0

4

_max, МПа

3,6

4,8

48,3

49,38

vрад

0,012

0,017

0,036

0,039

Рис.5.4. Расчётная схема (а) и эпюры крутящего момента (б), максимальных касательных напряжений (в) и углов закручивания (в)поперечных сечений бруса

моменты выражать через внеш­ние момен­ты, при­ло­женные с той стороны от рассмат­риваемого сечения, с которой расположен свобод­ный конец. Это позволяет определять крутящие моменты, не

вычисляя реактивного момен­та, возни­ка­ющего в за­делке. При этом принимаем следующее пра­ви­ло знаков: крутящий момент считается положительным, если он направлен по часовой стрелке при взгляде на рассматриваемую часть бруса со стороны отброшенной части. В связи с этим имеем по участкам (рис. 5.4, а) :

участок I: М_I = T₄ = 0,1 (кН м) ;

участок II: М₂ = T₄ - T₃ = 0,1 - 1,1 = -1,0 (кН м) ;

участок III: М₃ = T₄ - T₃ + T₂ = 0,1- 1,1 + 2,1 = 1,1 (кН м) ;

участок IV: М₄ = T₄ - T₃ + T₂ - T₁ = 0,1- 1,1 + 2,1 -5,1 = -4,0 (кН м).

Эпюра крутящих моментов приведена на рис. 5.4, б. Из неё видно, что в местах приложения внешних моментов происходит скач­ко­образное измене­ние значения внутреннего силового фактора.

2

3

. Исходя из условия статической прочности вала при кручении (_max  []), диаметр вала на каждом его участке опреде­ляет­ся по формуле

d   5 М_К /[]

По условию вал состоит из двух участков с диаметрами d₁ и d₂. Величина каждого из них определяется по указанной формуле, где в качестве М_К подставляется наибольшее из значений крутящего момента на соответст­ву­ющем участке. Поэтому в данном случае имеем

3

3

d ₁   5 М₄ /[] =  5·4·10³/(50 ·10⁶) = 0,0737 (м),

3

3

d 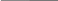₂   5 М₂ /[] =  5 ·1·10³/(50·10⁶) = 0,0464 (м).

3. Крутящий момент, действующий в сечении, является резуль­тирующим моментом внутренних сил, распределённых по сечению. Интенсивность распределения этих сил характеризуется ве­ли­­чиной касательных напря­жений, лежащих в плоскости попе­речного сечения и направленных перпен­дикулярно радиусу, соеди­няю­щему точку приложения силы с центром сече­ния. Численное значение этих напряжений прямо пропор­цио­нально рассто­янию точки их приложения от центра сечения. По полученным расчётным данным строим эпюру мак­си­мальных касательных напряжений (рис. 5.4, в).

4. Полный угол закручивания стержня, рад

v

l

z

=  M_K/ (GI_P) dz .

П

0

олярный момент инерции сечения вала I_P=d⁴/32. Так как крутящий момент в сечениях одного участка бруса не изменяется, то угол закручи­вания (рад) в пределах каждого участка может быть найден по формуле

v = M_K z / (GI_P).

Для бруса ступенчатого строения с цилиндрическими участ­ками формула для определения угла закручивания поперечных сечений имеет вид:

v

i

=  M_Ki l_i / (GI_Pi) .

Рассчитаем значения углов закручивания сечений бруса на границах участ­ков IV-I:

v_IV = M₄ ·a /(GI_P1)= - 4 ·10³ ·1 ·32/(8·10¹⁰ ·3,14 ·0,07374)=-0,017 рад.

v_III = v_IV + M₃ b / (GI_P1) = 0,012 рад,

v_II = v_III + M₂ c / (GI_P2) = 0,039 рад,

v_I = v_II + M₁ a / (GI_P2)= 0,036 рад .

По результатам расчётов строим эпюру углов закручивания поперечных сечений бруса (рис. 5.4, г).

Кручению подвергаются витки винтовых пружин, работающих на сжатие (рис. 5.5), в свобод­ном состоянии между вит­ка­ми должны быть зазоры, обес­пе­чи­ва­ю­щие требу­емую дефор­ма­цию пру­жин. При отношении H/D_СР  3 во избежание выпу­чивания ­ пружи­на сжатия должна работать в направ­ля­ющих. Конце­вые витки пру­жин сжатия подги­баются и шлифуются. У винтовых пружин, ра­бо­­тающих на растяжение, в сво­бод­ном состоянии витки обычно при­­жаты друг к другу. Жёсткость вин­товых пружин умень­ша­ется с уве­ли­че­ни­ем отношения D_СР/d=С, которое называется индексом пружины.

Цилиндрические винтовые пру­жи­ны рассчитываются из усло­вия проч­нос­ти витка пружины на кручение τ≤. Диаметр проволоки находится по формуле

d  8 P₃ C k^’/ ,

где Р₃- предельно допустимая нагрузка, С-индекс пружины (обычно С=5÷10), k’-коэф­фициент, учитывающий увеличение напряжений на внутренней стороне витка при уменьшении С, k’≈(4C+2)/(4С-3), -допускаемые касательные напряжения, в зависимости от класса пружины их значения находятся в пределах =300÷900 МПа.

По рассчитанному значению d подбирают ближайшее стандартное значение диаметра. Деформация (ход) всей пружины, по которой судят о величине действующей на пружину силе:

f=8С³ Р n /(Gd),

где n- число витков пружины, Р- осевая нагрузка на пружину, G- модуль упругости второго рода (≈ 8·10¹⁰ Па).

Жёсткость пружины

К = Р/f = G d⁴ /8 D³ n .

Рассмотрим пример расчёта цилиндрической пружины как преобразователя прибора определённого класса точности.

Задача. Определить геометрические параметры пружины сжатия с индексом С=6, используемой для измерения нагрузки величиной 30 кН при допустимой относительной пог­реш­ности снятия отсчёта, равной ε = 0,5 % (класс точности прибора 05).

Решение. Для упругого восприятия нагрузки Р-30000 Н необходимо, чтобы пружина имела диаметр d проволоки, превышающий значение

d  8 P₃ C k^’/ = 8 ·30000 6·(46+2)/(46-3)/3,14·900·10⁶ =

= 0,0251 м, принимаем d = 30 мм .

Абсолютная погрешность ∆X в определении деформации пру­жины равна половине длины деления шкалы отсчётного уст­ройст­ва. Если в качестве таковой использовать обычную линейку с длин­ной деления 1мм (что соответствует параметрам отсчётного устройства лабораторной установки с соответствующим классом точности), то соответствующая условиям задачи точ­ность измерения будет обеспечена при деформации пружины, равной

f = ∆X/ε ·100% = 0,5/0,5 · 100 = 100 мм

Минимальное количество n витков пружины, необходимое для получения ею такой деформации

n = fGd/(8С³Р) = 0,1· 8·10¹⁰·0,03/(8·6³·30000) = 4,63 ≈ 5

Прямые измерительные пружины (подвесы, растяжки), работающие на кручение, применяются в точных измерительных приборах для создания противодействующих моментов и выпол­нения функций опор подвижных систем приборов. Подвесы пред­ставляют собой сво­бодно висящую (строго верти­каль­но) упругую нить (пря­мую пру­жи­ну), на нижнем конце которой укреплена подвижная система прибора. Растяжки пред­ставляют собой метал­личес­кие уп­ру­гие нити (прямые пру­жины), кото­рые растягиваются и прикреп­ляются к корпусу приборов пос­ред­ством пружин-рессор. На растяжках подвешивается под­виж­ная си­с­тема прибора. Креп­ление на рессо­рах предохра­няет подвесы и растяжки от обрывов при ударах, толчках и вибрации и позволяет путём изменения рас­­тягивающей силы регулировать ве­ли­чи­ну противо­дейст­вую­щего момен­та.