24) Оптимальная фильтрация случайных сигналов

Фазочастотная характеристика фильтра
нулевая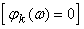 ,
следовательно, нет задержки по времени
и сохраняются фазовые соотношения,
имевшиеся во входном сигнале.
,
следовательно, нет задержки по времени
и сохраняются фазовые соотношения,
имевшиеся во входном сигнале.
В области частот, где полезный сигнал
намного сильнее шума, имеем коэффициент
передачи
 .
Там же, где сигнал слабый, коэффициент
передачи
.
Там же, где сигнал слабый, коэффициент
передачи
 .
Если на какой-либо частоте спектральные
плотности мощности сигнала и шума
одинаковы
.
Если на какой-либо частоте спектральные
плотности мощности сигнала и шума
одинаковы ,
то коэффициент передачи на этой частоте
равен 0,5.
,
то коэффициент передачи на этой частоте
равен 0,5.
Таким образом, оптимальный фильтр
пропускает те частоты, на которых сигнал
сильнее шума, и подавляет те, где он
слабее.
Отсутствие фазовых сдвигов обеспечивает
лучшее сохранение формы полезного
сигнала.
.
Определим, чему равна дисперсия ошибки
воспроизведения полезного сигнала для
оптимального фильтра. Подставив (3) в
(2), получим спектральную плотность
мощности сигнала ошибки:


 .
.
Дисперсия, равная значению корреляционной
функции при ,
может быть рассчитана с помощью теоремы
Винера-Хинчина:
,
может быть рассчитана с помощью теоремы
Винера-Хинчина:
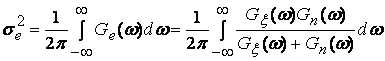 . (4)
. (4)
Пусть полезный случайный сигнал имеет
спектральную плотность мощности вида
 ,
,
где
 и
и ,
а шум является белым и имеет спектральную
плотность мощности
,
а шум является белым и имеет спектральную
плотность мощности
 (рис. 1, а).
(рис. 1, а).
Найдем характеристики оптимального
фильтра и рассчитаем дисперсию ошибки
воспроизведения полезного сигнала.




 .
.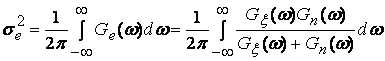 . (4)
. (4) ,
,