22)Отношение сигнал /шум на входе и выходе согласованного фильтра
Определим отношение сигнал/шум на входе
и выходе согласованного фильтра,
воспользовавшись определением (1). В
качестве модели для
мы использовали белый шум, дисперсия
которого бесконечно велика, поэтому
и
.
Для того чтобы найти выходное отношение сигнал/шум, необходимо предварительно определить вид полезного выходного сигнала. Сигнал на выходе линейной стационарной цепи с импульсной характеристикой определяется как
.
Подставим сюда выражение (7) для импульсной характеристики:
,
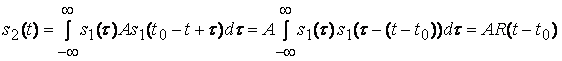где
– корреляционная функция сигнала
.
Таким образом, выходной сигнал
согласованного фильтра представляет
собой (с точностью до масштабного
множителя А) сдвинутую во времени
на
корреляционную функцию сигнала
.
Как известно, максимальное значение
корреляционной функции детерминированного
сигнала достигается при
и равно его энергии:
,
где
– энергия сигнала
.
Вывод:
Максимальное значение сигнала на выходе
согласованного фильтра достигается
при
и равно
.
Теперь необходимо рассчитать уровень шума на выходе. Спектральная плотность мощности шума на выходе линейной цепи может быть получена путем умножения спектральной плотности мощности входного шума на квадрат модуля коэффициента передачи:
,
где
– двусторонняя спектральная плотность
мощности входного белого шума. Дисперсия
определяется через интеграл от выходного
спектра шума:
.
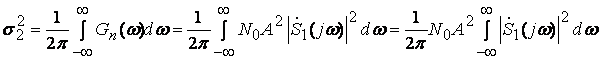Но, согласно равенству Парсеваля
.
Окончательно для среднеквадратичного значения шума получаем
.
Теперь можно получить выходное отношение сигнал/шум:
.
Вывод:
Отношение сигнал/шум на выходе согласованного фильтра не зависит от формы обрабатываемого сигнала, а определяется лишь его энергией и спектральной плотностью мощности входного белого шума.
23) Оптимальная фильтрация при небелом шуме. Критерий оптимальности
Простейшее и само собой напрашивающееся
решение состоит в том, чтобы предварительно
«обелить» шум, с помощью фильтра,
коэффициент передачи которого
выбран так, чтобы компенсировать
неравномерность спектра входного шума
(рис. 1).
Найдем, коэффициент передачи которого :
и, следовательно,
,
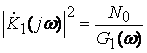(1)
где – произвольная константа.
Полезный сигнал
на выходе этого фильтра будет, очевидно,
иметь спектральную плотность, равную
.
(2)
Итак, на выходе «обеляющего» фильтра
мы имеем белый шум со спектральной
плотностью мощности
и измененный полезный сигнал
.
Так как шум белый, можно использовать фильтр, согласованный с сигналом комплексный коэффициент передачи которого, согласно , равен
,
где
– длительность сигнала
на выходе первого фильтра;
(
–
длительность входного сигнала).
Общий коэффициент передачи полученной таким образом системы будет равен
Воспользовавшись
(1), окончательно имеем
.
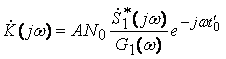Фильтр
,
оптимален для обнаружения сигнала
в белом шуме, но еще неизвестно, является
ли полученная таким образом составная
схема в целом оптимальной для решения
первоначально поставленной задачи,
т.е. для обнаружения сигнала
в шуме со спектром
.
Докажем оптимальность схемы рис. 1
методом «от противного».
Предположим, что существует фильтр с
коэффициентом передачи
,
обеспечивающий при подаче на вход
аддитивной смеси сигнала
и шума со спектральной плотностью
большее выходное отношение сигнал/шум,
чем схема, показанная на рис. 1. Представим
коэффициент передачи такого фильтра в
виде
.
Пусть
является коэффициентом передачи
«обеляющего» фильтра, т.е. удовлетворяет
условию (1). На выходе этого фильтра будет
получен сигнал
и белый шум со спектральной плотностью
,
т.е. те же условия, что и на выходе первого
фильтра на рис. 1.
Так как отношение сигнал/шум на выходе,
согласно сделанному предположению,
должно быть больше, чем для рассмотренной
схемы (см. рис. 1), то фильтр с комплексным
коэффициентом передачи
обеспечивает при подаче на вход аддитивной
смеси сигнала
и белого шума большее отношение
сигнал/шум, чем фильтр, согласованный
с сигналом
,
что невозможно. Полученное противоречие
доказывает, что схема, показанная на
рис. 1, имеющая коэффициент передачи
(3), действительно является оптимальной
для обнаружения детерминированного
сигнала в шуме с известной спектральной
плотностью мощности.
Рассчитаем для данного случая выходное
отношение сигнал/шум. Так как второй
фильтр согласован с сигналом
то, в соответствии с
,
это отношение может быть представлено
как
,
(4)
где
– энергия сигнала
,
а
– спектральная плотность белого шума
после «обеляющего» фильтра.
Согласно равенству Парсеваля энергия сигнала может быть рассчитана и в спектральной области:
.
Подставив в выражения
для спектра
и
для коэффициента передачи
,
имеем
.
Таким образом, в общем случае выходное отношение сигнал/шум определяется «взвешенной» в частотной области энергией обрабатываемого полезного сигнала; весовая функция при этом обратно пропорциональна спектральной плотности мощности шума.
Замечание. Легко видеть, что при
формула (5) превращается в полученное
ранее для случая белого шума выражение