
- •Міністерство освіти і науки, молоді і спорту україни Національний авіаційний університет
- •Курсова робота
- •1. Мета курсової роботи
- •2. Завдання на курсову роботу
- •3. Теоретичні відомості
- •Структурна схема одноплатного мікроконтролера
- •3.2. Генератор псевдовипадкових чисел
- •3.2.1. Лінійна конгруентна послідовність
- •3.2.2. Вибір модуля
- •3.2.3. Вибір множника
- •3.2.4. Вибір збільшення
- •3.2.5. Остаточний вібір значень
- •4. Програмна реалізація
- •4.1. Текст програми
- •4.2. Алгоритм програми
- •5. Перелік літератури
3.2.3. Вибір множника
Коли період послідовності має довжину m, кожне число від 0 до (m-1) зустрічається за період рівно один раз. Тому вибір початкового значення X0 не впливає на довжину періоду. Для забезпечення лінійної конгруентної послідовності максимальної довжини необхідно, щоб:
a,c і m, були взяємно простими числами;
якщо m являє собою степінь двійки (тобто процессор працює в двійковій системі числення), то вибираємо множник тамким, щоб
a mod 8 = 5;
множник а повинен перевищувати величину √m, бажано, щоб він був більше m/100, але менше m-√m.
У таблиці 3 наведені 10 значень множників, які задовольняють приведеним вище критеріям, що накладаються на вибір множника а для лінійної конгруентної послідовності при m=8191.
Таблиця 3.
a0 |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
101 |
107 |
131 |
157 |
163 |
173 |
179 |
197 |
211 |
227 |
3.2.4. Вибір збільшення
Вище було визначено, що с і m повинні бути взаємно простими числами. У таблиці 4 приведені значення збільшень с, які задовольняють приведеним критеріям з похибкою не більше 1%.
Таблиця 4.
Збільшення |
Значення |
Похибка % |
с1 |
1721 |
-0.57 |
с2 |
1723 |
-0.46 |
с3 |
1733 |
+0.12 |
с4 |
1741 |
+0.58 |
с5 |
1747 |
+0.93 |
3.2.5. Остаточний вібір значень
Для спрощення написання програми на АСЕМБЛЕРІ 1810, поставимо перед собою критерій: псевдовипадкове число повинно знаходитись у діапазоні [0,255], а в бенкер генератора повинно бути записано 10 псевдовипадкових чисел.
У ролі модуля, збільшення, множника візьмемо: a=101, c=1733, m=8191. Так як від початкового значення X0 період послідовності не залежить, а наш критерій [0,255], то потрібно взяти його з цього діапазону, довільним. Нехай це будет число X0=157
![]()
![]()
![]() обудуємо
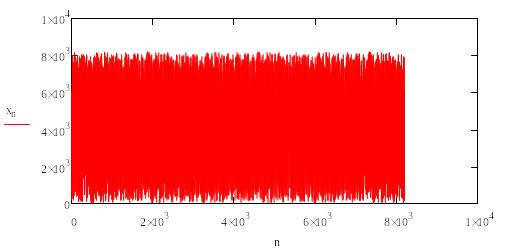
математичну модель нашої послідовності:
обудуємо
математичну модель нашої послідовності:
![]()
4. Програмна реалізація
4.1. Текст програми
TITLE
SSEG SEGMENT PARA STACK 'STACK'
DB 256 DUP(0)
SSEG ENDS
DSEG SEGMENT PARA PUBLIC 'DATA'
a Dw 1 DUP(131)
c DW 1 DUP(1733)
m DW 1 DUP(8191)
x DW 1 DUP(157)
DSEG ENDS
CSEG SEGMENT PARA PUBLIC 'CODE'
ASSUME CS:CSEG,DS:DSEG,SS:SSEG
General PROC FAR
mov ax,DSEG
mov di,ax
Start: mov si,0
mov ax,0
clc
mov ax,x
mov bx,a
k: mul WORD PTR[bx]
add ax,c
sub m,ax
abc: cmp ax,m
jb stasiuk
mov ax,dx
sub m,ax
loop abc
stasiuk: mov [si],dx
cmp si,10
jnb olia
inc si
mov ax,dx
jmp k
olia: jmp Start
General ENDP
CSEG ENDS
END General
