65. Непрерывность функции в точке и на промежутке. Классификация точек разрыва. Непрерывность функции

Рассмотрим функцию , определенную на промежутке Пусть . Функция называется непрерывной в точке , если

Функция называется непрерывной слева (справа) в точке , если . Естественно, при этом функция должна быть определена в некоторой окрестности слева (справа) то точки . Непрерывность функции в точке означает непрерывность этой функции в указанной точке как слева, так и справа.

Функция , определенная на интервале называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала .

Функция

Точки разрыва

Непрерывность функции в точке , т.е. выполнение условия (3), означает, что оба односторонних предела и существуют и равны , т.е. .

Если условие (4) не выполнено, то точку называют точкой разрыва функции . Условие (4) означает выполнение следующих четырех условий, каждое из которых предполагает выполнение всех предыдущих:

1. и существуют;

2. и конечны;

3. ;

4. .

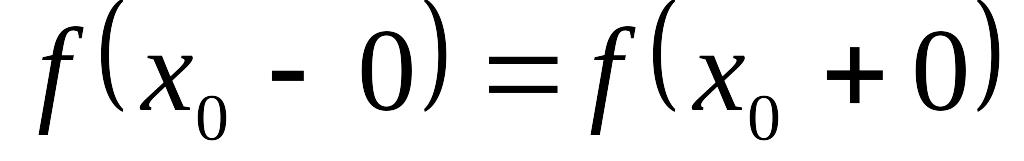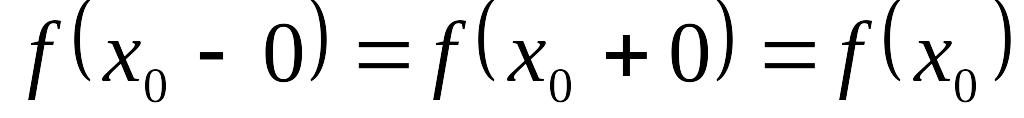Если 1. не выполнено, то называют точкой неопределенности.

Если 1. выполнено, а 2. не выполнено, то называют точкой бесконечного скачка.

Если выполнены 1. и 2., а 3. не выполнено, то называют точкой конечного скачка. Величина называется скачком функции в точке _.

Если 1., 2., 3. выполнены, а 4. не выполнено, то называют точкой устранимого разрыва.

Если функция определена в окрестности точки и не определена в самой точке , то также называют точкой разрыва. Такие точки классифицируют по той же схеме.

66. Основные теоремы о непрерывности функции

Теорема (первая теорема Больцано–Коши). Пусть функция определена и непрерывна на отрезке , и на концах этого промежутка принимает значения разных знаков; тогда найдется точка , в которой функция равна нулю.

Теорема (вторая теорема Больцано–Коши). Пусть функция определена и непрерывна на отрезке . Тогда, если то функция принимает все свои промежуточные значения, принадлежащие промежутку , где , , т.е. .

Теорема (первая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция является ограниченной на этом отрезке.

Теорема (вторая теорема Вейерштрасса). Пусть функция определена и непрерывна на отрезке , тогда функция имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).

67. Свойства функции непрерывной в точке. Непрерывность элементарных функций.

, определенная на отрезке ( ) называется непрерывной на отрезке , если она непрерывна в каждой точке интервала , непрерывна справа в точке и непрерывна слева в точке .