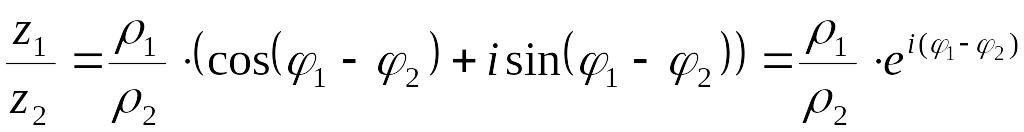№1 Множества и действия над ними.

Множество представляет собой соединение, совокупность, собрание некоторых предметов, объединённых по какому-либо признаку. Предметы из которых состоит множество, называется его элементами. αєА – означает, что элемент αпринадлежит множеству А. Множества, состоящие из одних и тех же элементов, называются равными.

Если любой элемент множества В является и элементом множества А, то множество В называется подмножеством. ВєА.

Пусть даны 2 множества А и В. Множество С, которое состоит из всех элементов множества А, не принадлежащих множеству В, называется разностью множеств А и В. И записывается как А/В.

Пересечение множеств – Множество С, состоящие из всех тех и только тех элементов, которые принадлежат каждому из данных множеств А и В, называется пересечением множеств А и В. Обозначается А

№2 Метод математической индукции.

Предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены следующие 2 условия:

Предложение p(n) истинно для n=1

Для любого натурального K из предложения, что p(n) истинно n=k, следует что оно истинно и для n=K+1

Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения p(n) для всех натуральных значений n, то сначала проверяют истинность предложения p(1) и затем, допустив истинность высказывания p(k), доказывают истинность высказывания p(k+1). Если высказывания p(1) истинно и для каждого натурального значения k из предложения истинности p(k+1), то в соответствии с принципом мат. индукции предложение p(n) является истинным для всех значений n.

№3 Сочетание. Формула числа сочетаний

Сочетанием из n элементов по k элементам называется любое подмножество из k элементов множества содержащего n элементов.

Число сочетаний из n элементов по k обозначается C_n^k вычисляется по ф-ле:

, где n – это произведение последовательных натуральных чисел от 1 до n.

№4 Бином Ньютона.

Ньютоном была выведена ф-ла для вычисления любой натуральной степени двучлена (a+b), эта ф-ла называется Биномом Ньютона. Она имеет вид:

Эта ф-ла доказывается методом мат. индукции. Ф-ла общего члена Бинома Ньютона имеет вид:

Сумма всех биномиальных коэффициентов разложения

№5 Действительные числа. Модуль действительного числа.

Числовые множества. Множество Q всех рациональных чисел и множество J всех иррациональных чисел образуют множество R действительных (вещественных) чисел.

№6 Комплексные числа.

– мнимая единица, т.е.

a+bi, где a и b действительные числа называется комплексным числом

a+bi и –a-bi – противоположные

a+bi и a-bi – сопряжённые

а – называется действительная часть комплексного числа

b – коэффициент при мнимой части

Операции над комплексными числами:

Сложение

Z1+Z2=a+bi+c+di=(a+c)+(b+d)i

Вычитание

Z1-Z2=a+bi-(c+di)=(a-c)+(b-d)i

Умножение

Z1*Z2=(a+bi)*(c+di)=ac-bd+(ad+bc)i

Деление

Z1/Z2=(a+bi)/(c+di)= i

№7Геометрическая интерпретация комплексного числа.

Каждому комплексному числу Z=a+bi соответствует пара действительных чисел a и b,а каждой паре действительных чисел на плоскости соответствует единственная точка с координатами a и b. Таким образом, комплексные числа можно изображать точками плоскости a на OX и b на ОУю.

OX- действительная OY- мнимая

№8Операции над комплексными числами

Алгебраическую операцию сложения на множестве можно задать следующим образом:

.

Сложение комплексных чисел ассоциативно, т.е. и коммутативно, т.е. . Сумма чисел , поэтому число является противоположным числу , тем самым определена операция вычитания .

Учитывая, что через обозначен корень уравнения , т.е. или , можно определить умножение комплексных чисел:

.

Умножение также ассоциативно и коммутативно. Произведение нескольких сомножителей вычисляется как последовательное умножение. Натуральная степень комплексного числа может быть найдена при помощи формулы бинома Ньютона. Поскольку , , , , , при возведении в любую натуральную степень , надо найти остаток от деления на 4 и возвести в степень, равную этому остатку.

Чтобы определить деление комплексных чисел, нужно определить число обратное числу . Для действительного числа обратным будет число .

Выражение 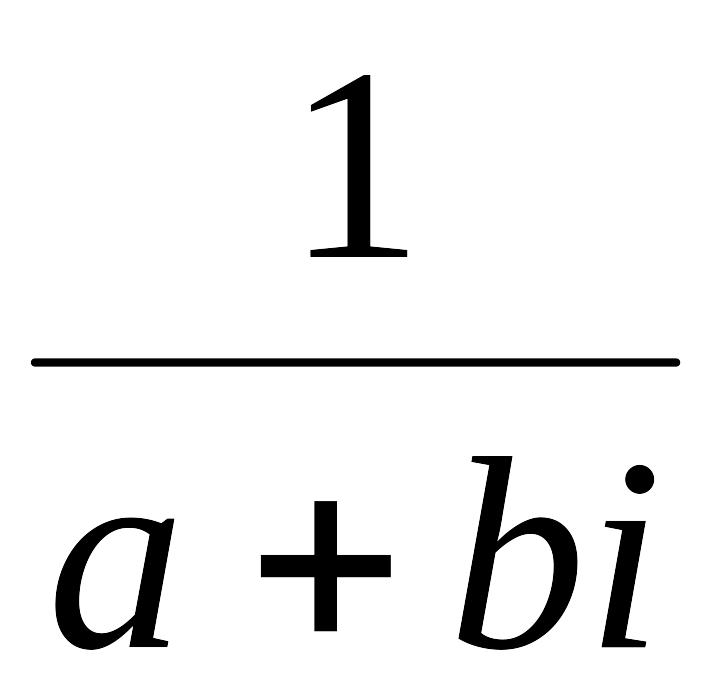запишем в стандартной форме. Для этого умножим числитель и знаменатель на комплексное число :

,

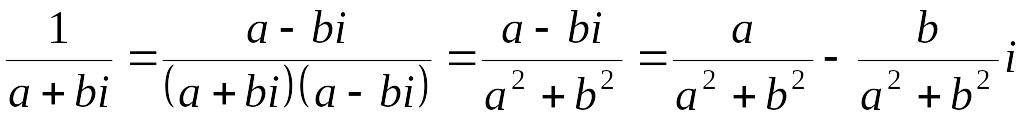где .

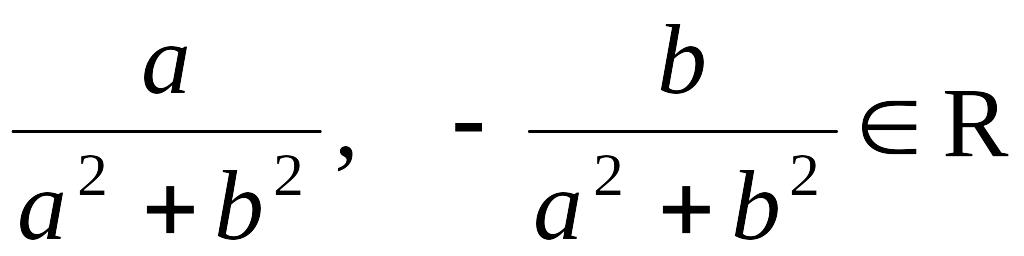Значит, для любого ненулевого комплексного числа существует обратное. Таким образом, операция деления определена как произведение делимого на число, обратное делителю.

Множество комплексных чисел является расширением множества действительных чисел, любое действительное число можно записать в виде .

Число называется сопряженным числу и обозначается .

Сумма и произведение сопряженных чисел являются числами действительными:

;

.

Число называется модулем или абсолютной величиной комплексного числа . Очевидно, что .

Свойства сопряжения:

;

.

Каждому комплексному числу поставим в соответствие точку плоскости, координатами которой в прямоугольной системе координат являются числа и .

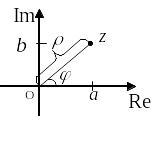
Рис. 3.1.

Тогда каждой точке плоскости будет соответствовать единственное комплексное число . В результате получается взаимно однозначное соответствие между множеством комплексных чисел C и множеством точек плоскости, которое позволяет отождествить произвольное комплексное число с точкой плоскости, имеющей в выбранной системе координат координаты . При этом точки горизонтальной координатной оси изображают действительные числа и поэтому эту ось называют действительной осью, а по вертикальной оси откладываются мнимые части комплексных чисел, поэтому вертикальная ось называется мнимой осью.

Расстояние от точки до начала координат есть действительное неотрицательное число , которое называется модулем комплексного числа и обозначается . Угол между положительным направлением действительной оси и радиус-вектором точки называется аргументом и обозначается . Для числа 0 аргумент не определен, для остальных комплексных чисел аргумент определяется с точностью до целых кратных , при этом положительные углы отсчитываются против часовой стрелки.

Пусть . Из рис. 3.1 ясно, что модуль числа находится по формуле . Аргумент числа определяется из равенств , .

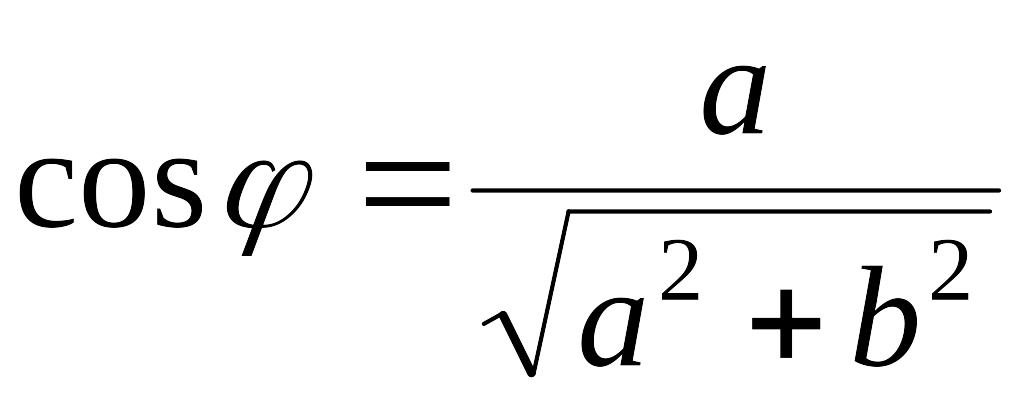Отсюда:

(3.1)

№9Тригонометрическая форма комплексного числа.Запись числа в виде (3.1) называется тригонометрической

формой комплексного числа.

Если воспользоваться формулой Эйлера,

(3.2)

то от тригонометрической формы записи комплексного числа (3.2) несложно перейти к его показательной форме записи:

.

Пусть и ‑ сопряженные числа. Если , то . Геометрически и являются точками, симметричными относительно действительной оси (рис. 3.2). Отсюда вытекают равенства .

b

-

a



у

х





b

Рис. 3.2.

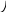
Перемножать и делить комплексные числа удобнее, если они представлены в тригонометрической форме:

(3.3)

В показательной форме:

При умножении комплексных чисел их аргументы складываются, а модули перемножаются. Это правило верно для любого числа сомножителей.

Аналогично,

(3.4)

При выполнении деления комплексных чисел в тригонометрической форме их аргументы вычитаются, а модули нужно разделить.

№10Показательная форма комплексного числа.

Эйлером было установлено, что cosφ+sinφ=eiφ, тогда комплексное число z=r(cosφ+isinφ) можно записать в виде , где e~2,73

10. Показательная форма комплексного числа.

Эйлером было установлено что cosβ+isinβ=e^iβ, тогда комплексное число z=2(cosβ+isinβ) можно записать в виде z=2*e^iβ(показательная формула, е=2,73…).

11.Алгебраические многочлены. Теорема Безу.

Функция f(x)=A₀xⁿ+А­₁x^n-1+…+ A_n, где n-целое число, как известно, называется многочленом или целой частью рациональной функцией от х; число n называется степенью многочлена. A₀, А­_1, A_n- действительные или комплексные числа.

Теорема Безу. При делении многочлена f(x) на разность х-а получается остаток равный F(a).

Следствие. Если а есть корень многочлена, т.е. f(a)=0, то f(x) делится без остатка на х-а и, следовательно, представляется в виде произведения f(x)=(x-a)f₁(x),где f₁(x)-многочлен.

Основная теорема алгебры. Всякая целая рациональная функция f(x) имеет по крайней мере хотя бы один корень, действительный или комплексный.

Теорема3. Всякий многочлен n-степени разлагается на n линейных множителей вида х-а и множитель, равный коэффициенту при хⁿ.

Теорема. Если многочлен f(x) с действительными коэффициентами имеет комплексный корень а+ib, то он имеет сопряженный корень a-ib.

12. Векторный базис на плоскости и в пространстве. Декартова система координат на плоскости и в пространстве.

Векторным базисом на плоскости называют два произвольных неколлинеарных вектора этой плоскости, взятых в определенном порядке.

Система координат на плоскости и в пространстве.

Совокупность фиксированной точки О и ….. базиса (i;j) называется декартовой системой координат на плосксти.

Совокупность точки О, луча ОР и единого вектора е называются полярными координатами.

13.Скалярные и векторные величины. Линейные операции над векторами.

Величины, которые в выбранной системе единиц вполне ха-ся заданием их численных значений называются скалярными, а если этих значений не достаточно –векторными.

Линейные операции над векторами - это операции сложения и вычитания векторов и умножение вектора на число.

14.Операции над векторами, заданными своими координатами.

Координаты суммы(разности) двух векторов равны сумме(разности)одноименных координат этих векторов.

При умножении вектора на число на это число умножаются его координаты.

Скалярное произведение двух векторов равно сумме произведений одноименных координат.

Модуль вектора равен корню квадратному из суммы квадратов его координат.

15.Скалярное произведение векторов и его свойства.

Определение 1: скалярным произведением двух отличных от нуля векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов равен нулю, то скалярное произведение этих векторов равно нулю. Скалярное произведение векторов а и b обозначается а* b, или аb, или(а,b). Итак, по определению

_ _

аb=|a|*|b|*cos fi, где fi=(а, b).

Определение 2: проекцией вектора а на ось L называется число, равное произведению модуля вектора а на косинус угла между вектором а и осью L и обозначается

_ _

прbа=|a|cos(a,L).

Скалярное произведение двух векторов обладает следующими свойствами:

Свойство коммутативности: ab=ba.

Это свойство вытекает непосредственно из определения скалярного произведения.

Числовой множитель можно выносить за знак скалярного произведения, т.е:

(/\а)b=a(/\b)=/\(ab).

Свойство дистрибутивности: a(b+c)=ab+ac. 2 2

Скалярный квадрат вектора а*а равен квадрату модуля этого вектора, т.е. а =|a| .

Скалярное произведение двух ненулевых векторов а и b равно нулю тогда и только тогда, когда а _|_ b.