6. Обчислення площ геометричних фігур за методом монте-карло

Метод Монте-Карло появився практично одночасно із створенням в 1949р. першої лампової ЕОМ універсального призначення MARK-1 (Манчестерський університет, Англія). Теоретичні основи такої ЕОМ були закладені Дж. Нейманом. Дж. Нейман разом з С. Уламом запропонували перший варіант методу Монте-Карло у зв'язку із роботою по розрахунку ядерних реакторів. Ефективне застосування методу Монте-Карло, завжди пов'язане з "використанням" величезної кількості чисел, стало можливим тільки завдяки застосуванню комп'ютерів.

Новим методом швидкого зацікавилися фізики. Перше успішне застосування його до розрахунку рівнянням стану рідини, "описано в роботі Н. Метрополіса.

Метод Монте-Карло налягає у генеруванні за допомогою ЕОМ випадкових процесів з різними властивостями. Ці процеси використовуються для розв'язування конкретних обчислювальних задач.

Метод статистичних випробувань (Метод Монте-Карло) — чисельний метод. застосований на моделюванні випадкових величин і побудови статистичних оцінок для шуканих величин.

Інтегруюча назва методу Монте-Карло до знаменитого казино відношення немає. Хіба що ігрова рулетка може бути використана як датчик рівноймовірних випадкових чисел. Це дуже повільний датчик. Комп'ютер генерує випадкові числа практично миттєво.

Метод Монте-Карло можна, зокрема, застосувати до обчислення площ геометричних фігур.

Нехай треба обчислити площу деякої геометричної фігури F.

мал. 7

Помістимо фігуру F у деякий прямокутник (мал. 7) і будемо рівномірно покривати його випадковими точками. Нехай для цього було використано п точок Підрахуємо, скільки із цих точок попало на фігуру F. Нехай, наприклад п1. Оскільки покриття прямокутника і фігури випадковими точками

здійснювалося рівномірно, то можна зробити висновок, що числа n₁ i n пропорційні площинам фігури S_F і прямокутника S_p. Отже , звідки.

Досліджено, що ця формула дає точний результат, якщо n. Отже, беручи велику кількість точок (число n), можна обчислити площу фігури F з потрібною нам точністю.

Приклад. Обчислити методом Монте-Карло площу еліпса, півосі якого а та b (мал. 8).

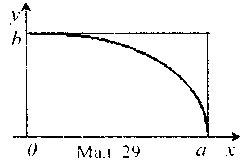
Точка з координатами (x, у) належить прямокутнику, якщо виконуються умови: 0 ≤ х ≤ a; 0 ≤ y ≤ b.

Точка з координатами (х, у) належить 1/4 еліпса, якщо виконуються умови

мал. 8

Складаємо алгоритм розв’язування задачі: (мал. 9).

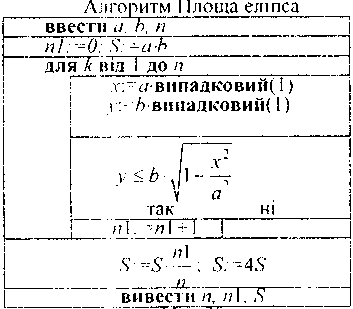
мал. 9

Кодуємо цей алгоритм на мові Паскаль.

Реалізувавши цю програму при n=300, 500, 1000; a=1,5; b=1 відповідно дістанемо такі результати:

n	n1	S
300	211	4.22
500	398	4.776
1000	787	4.722

Обчисливши площу цього еліпса за формулою , дістанемо Отже, вже при тисячі випадкових точок матимемо практично задовільні результати.

Зазначимо, що цей метод вимагає величезної кількості обчислень і тому може бути ефективно реалізований тільки на досить швидкодіючих персональних комп’ютерах.