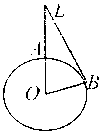3. Побудова аналітичних математичних моделей

Аналітична математична модель -— це модель, яка подається у вигляді формул, рівнянь чи нерівностей, систем рівнянь чи нерівностей і т.п.

Моделювання будь-якого об'єкту неможливе без попередньої формалізації.

Формалізація — це математична постановка задачі: процес виділення і переведення внутрішньої структури об'єкта у визначену інформаційну структуру —- форму.

Побудова математичної моделі передбачає встановлення зв'язків між параметрами процесу, виявлення його граничних і початкових умов та формалізації процесу у вигляді системи математичних співвідношень.

При побудові математичної моделі необхідно дотримуватися основного методологічного принципу: всі засади (посилки), на яких будується математична модель повинні бути строго доведені або перевірені, експериментально.

Нехтування цього принципу призводить до грубих помилок у моделюванні.

Побудова математичної моделі передбачає виконання таких етапів:

1) Чітко з'ясувати, що дано за умовою задачі. Які обмеження накладаються на вхідні дані?

2) Чітко з'ясувати, що треба знайти? Які умови повинні задовольняти результати?

3) Встановити зв'язки між вхідними даними (аргументами) і результатами у вигляді системи математичних співвідношень.

Приклад 1. Як далеко видно з літака до горизонту?

В процесі формалізації задачі робимо допущення, що Земля має форму ідеальної кулі (мал. 4), літак летить на відстані h від поверхні Землі, радіус якої R. Відстань від літака до горизонту - це довжина катета прямокутного трикутника. В процесі формалізації задачу зведено до суто математичної проблеми: обчислити катет прямокутного трикутника за гіпотенузою і другим катетом.

Maл. 4

OA = OB = R, AL = h, LA = l Тоді

Приклад 2. Визначити швидкість штучною супутника Землі, який обертається навколо її поверхні.

Побудуємо математичну модель, яка заснована на таких допущеннях (передумовах):

1) Земля мас форму кулі:

2) Штучний супутник обертається навколо Землі по коловій орбіті;

3) Опором повітря можна знехтувати.

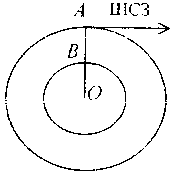
Виходячи з цих допущень можна побудувати малюнок (мал. 5).

Математичну модель розв'язування задачі можна записати за допомогою формул, що математично описують деякі основні закони механіки Ньютона.

Maл. 5

де т -— маса ШСЗ, М — маса Землі, G -- гравітаційна стала, v -— космічна швидкість. h — відстань ШСЗ від поверхні Землі.

Виконавши внутрішньомодельне розв'язання, остаточно одержуємо

4. Побудова дискретних математичних моделей

Дискретні математичні моделі — це такі моделі, в яких зв'язки між даними і шуканими елементами подаються на мові приростів (приросту часу, швидкості, довжини тощо).

Побудова дискретних математичних моделей здійснюється за тими ж етапами, що і аналітичних. При цьому ще використовується метод дискретизаці неперервних фізичних процесів.

Суть цього методу полягає в тому, що неперервний фізичний процес, який, наприклад, здійснюється в часі, замінюють дискретним. Наприклад, неперервний відрізок часу [t₁,t₂] розбивають на п рівних частин – квантів

Вважають, що на протязі одного кванту часу ніяких змін із величинами, що беруть участь в даному фізичному процесі не відбувається. Фізичні величини змінюються стрибкоподібно при переході від одного кванту часу до іншого. Тому дискретна математична модель описує стан фізичного процесу в один із моментів часу, а стан в наступний момент часу (через ∆t) визначається рекурентними співвідношеннями.

Приклад. Побудувати модель падіння тіла, враховуючи опір повітря.

Експериментально встановлено, що сила опору повітря пропорційна квадрату швидкості, а коефіцієнт залежить від форми тіла. Тому прискорення падаючого тіла має вид a=g-kv², де k — коефіцієнт, що залежить від форми і маси тіла (для людини середнього зросту і ваги k  0.004).

З фізики невідомо формул, що виражають падіння тіла з врахуванням опору повітря. Тому розіб'ємо час падіння на рівні проміжки ∆t і будемо вважати, що висота і швидкість змінюється скачкоподібно в кінці кожного інтервалу: t₁=0, t₂=∆t, t₃=2∆t і т.д. Нехай для, деякого моменту часу t відомі висота тіла h, і швидкість тіла v₁. Тоді Підрахуємо висоту і швидкість тіла через проміжок часу ∆r

при цьому вважаємо, що на проміжку часу ∆tv_і, і а_і не змінюються.

Записані співвідношення тим точніші, чим меншим є проміжок часу ∆t (чим менший інтервал, тим менше змінюються на ньому швидкість і прискорення). Одержані формули є рекурентними співвідношеннями, які подають наступний стан процесу через попередній.

Отже, шукана математична модель описується такими рекурентними співвідношеннями: або