Теорема об изменении количества движения точки

При решении многих задач динамики вместо интегрирования ДУД оказывается более эффективным использование т.н. общих теорем динамики.

Рассмотрим теорему об изменении количества движения точки. Количеством движения МТ называют величину 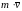, равную произведению массы точки на ее скорость. Вектор направлен по касательной к траектории точки.

Элементарным импульсом силы называют величину

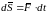, (4.4.1)

равная произведению силы на элементарный промежуток времени. Направлен импульс вдоль линии действия силы. Импульс 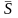силы за конечное время t₁

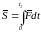(4.4.2)

Модуль и направление импульса можно вычислить по его проекциям

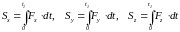. (4.4.3)

Основной закон динамики можно представить в виде

.

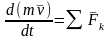Это теорема об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Та же теорема в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за этот промежуток времени

.

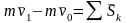При решении задач обычно пользуются уравнениями в проекциях.

Теорема об изменении момента количества движения точки

Моментом количества движения точки относительно некоторого центра О называется векторная величина 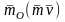, определяемая равенством

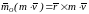
где — радиус-вектор движущейся точки, проведенный из центра О.

При этом вектор 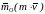направлен перпендикулярно плоскости, проходящей через 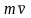и центр О, a .

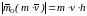Момент количества движения точки относительно какой-нибудь оси Оz, проходящей через центр О, равен проекции вектора на эту ось

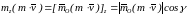
где  — угол между вектором 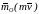и осью Оz.

Теорема: производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра

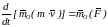
Теорема моментов относительно оси

.

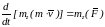Из уравнения (6.20) следует, что если 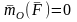, то .

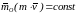Билет17. Теорема об изменении кинетического момента точки.

Теорема об изменении кинетического момента

При движении механической системы ее кинетический момент Ко изменяется с течением времени. Чтобы установить закон изменения кинетического момента, продифференцируем по времени обе части выражения

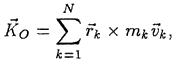
определяющего кинетический момент:

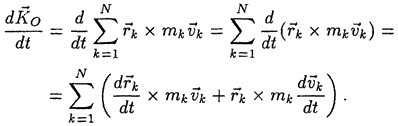
Билет18. Работа силы. Мощность. Теорема об изменении кинетической энергии точки.

Элементарной работой силы , приложенной в точке М (рисунок 4.1), называют скалярную величину

dW = F_ ∙ds,

где F_ — проекция силы на касательную М к траектории точки М, направленную в сторону перемещения точки;

ds — модуль элементарного перемещения точки М.

Т.к. ds = |d | (здесь d - вектор элементарного перемещения точки), то равенство dW = F_ ∙ds можно представить в виде

d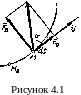 W= .

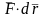т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения.

Работа силы на конечном перемещении M₀M₁ (рисунок 4.1) определяется как

,

.

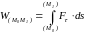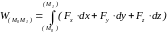Мощностью называют величину, равную работе, совершаемой силой в единицу времени. Если работа совершается равномерно, то мощность P = W/t₁ (здесь t₁ - время, течение которого произведена работа W). В общем случае

,

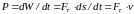т.е., мощность равна произведению касательной составляющей силы на скорость.

Кинетической энергией (КЭ) точки называют скалярную величину 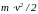. Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

.

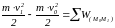Билет19. Механическая система. Силы внешние и внутренние. Масса системы. Центр масс. Дифференциальные уравнения движения системы.