Центр параллельных сил.

Рассмотрим систему параллельных сил  {F₁, F₂, ..., F_n}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а).

Эта точка называется центром параллельных сил. 

Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

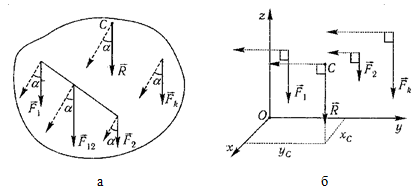
Рисунок 1.5

Для определения координат центра параллельных сил воспользуемся этой теоремой.

Относительно оси x 

 M_x(R) = ΣM_x(F_k),    _- y_CR = Σy_kFk        и        y_C = Σy_kFk /Σ_Fk.

Относительно оси y 

 M_y(R) = ΣM_y(F_k),       _- x_CR = Σx_kFk        и       x_C = Σx_kFk /Σ_Fk.

Чтобы определить координату  z_C, повернем все силы на 90° так, чтобы они стали параллельны оси  y (рисунок 1.5, б). Тогда

 M_z(R) = ΣM_z(F_k),        _- z_CR = Σz_kFk        и       z_C = Σz_kFk /Σ_Fk.

Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид

r_C = Σr_kFk /Σ_Fk.

Свойства центра параллельных сил:

1 Сумма моментов всех сил  _Fk  относительно точки  C  равна нулю   ΣM_C(F_k) = 0.

2 Если все силы повернуть на некоторый угол  α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой  C.

Центр тяжести твердого тела

На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести. Эти силы о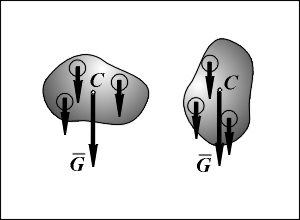 бразуют поле силы тяжести.

Для тел, размеры которых малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполнены эти два условия, называют однородным полем тяжести.

Равнодействующая G сил тяжести, действующих на частицы данного тела, называется весом тела. По модулю вес тела равен произведению его массы m на ускорение свободного падения g 9.81 м / c² : G = m · g.

Центром тяжести тела называется неизменно связанная с этим телом точка С, через которую проходят линии действия веса тела при любом положении тела в пространстве (см.рис.).

Такая точка всегда существует и является примером так называемого центра параллельных сил.

Центр тяжести тела является геометрической точкой, которая может распологаться вне пределов данного тела (например, для кольца).

Билет7. Способы задания движения точки. Вектор скорости точки. Вектор ускорения точки.

Способы задания движения точки

Движение точки может быть задано одним из трех способов.

1. Векторный способ. Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение точки в любой момент времени можно определить, задав ее радиус-вектор 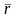(рисунок 3.1) как функцию от времени t

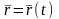
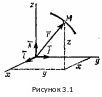. (3.2.1)

Это и есть закон движения точки в векторной форме.

2. Координатный способ. Положение точки можно непосредственно определять ее координатами, изменяющимися при движении с течением времени

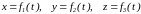. (3.2.2)

Э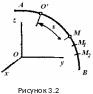 то - закон движения точки в прямоугольных декартовых координатах.

3. Естественный способ. Задать движение точки естественным способом – это задать (рисунок 3.2) ее траекторию, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде

.

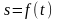Скоростью точки в данный момент времени t называется величина 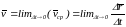, так что скорость есть первая производная от вектора по аргументу t:

.

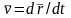Ускорением точки в данный момент времени t называют векторную величину, к которой стремится 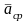при стремлении промежутка времени t к нулю

.

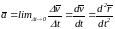т.е., вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени

Билет8. Определение скорости и ускорения точки при координатном способе задания движения.

Используем следующую теорему: проекция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось.

Тогда для проекций скорости имеем

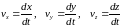
или .

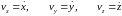т.е., проекции скорости точки на координатные оси равны первым производным от проекций соответствующих координат точки по времени.

Для проекций ускорения имеем

, ,

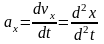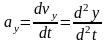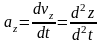
ил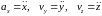и , т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.

Билет9. Оси естественного трехгранника. Числовое значение скорости. Касательное и нормальное ускорения точки.