Теоретическая Механика

ТЕОРИЯ

Билет1. Геометрический способ сложения сил. Геометрическое и аналитическое условия равновесия системы сходящихся сил.

П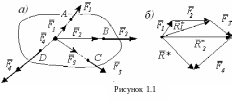 усть к телу в точках А, В, С, D приложены силы 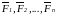, ЛД которых пересекаются в точке О (рисунок 1.1 а). Перенесем силы вдоль их ЛД в точку О и будем последовательно складывать силы по правилу силового треугольника (рисунок 1.1 б). Сначала найдем равнодействующую сил и , затем 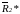сил и 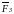и т.д. Получим следующее: 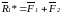, , 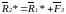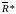= . Если сил n, то

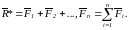
можно определить также, отложив вектор 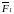и приложив к его концу вектор 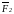, затем к концу - вектор , и т.д. Равнодействующая соединяет начало первого вектора с концом последнего.

Т.о., равнодействующая системы сходящихся сил равна векторной сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения ЛД слагаемых сил. Чтобы найти равнодействующую геометрическим способом, надо построить в точке пересечений их ЛД силовой многоугольник на слагаемых силах; замыкающая силового многоугольника будет равнодействующей.

Рассмотрим аналитический способ определения равнодействующей системы сходящихся сил. Спроецируем векторное равенство на оси прямоугольных координат и найдем проекции равнодействующей

, , .

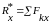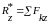Модуль равнодействующей силы определяется, как

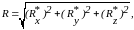
а направление - по трем направляющим косинусам

, , .

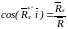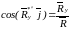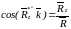Для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна нулю, т.е., 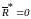или 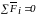(условия равновесия в векторном виде). Условия равновесия в геометрическом смысле выражаются в том, что силовой многоугольник должен быть замкнут, т.е., конец последнего вектора должен совпасть с началом первого вектора. В аналитическом виде они выражаются в том, что должны равняться нулю суммы проекций на три координатные оси всех сил, входящих в систему

, , .

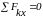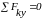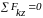Условия равновесия для плоской системы сходящихся сил

, .

Теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Билет2. Момент силы относительно центра и оси. Пара сил. Момент пары сил.

Моментом силы 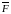относительно оси называется проекция векторного момента этой силы, взятого относительно любой точки оси, на эту ось, т. е.

.

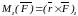
Проекция на ось момента силы , взятого относительно какой-либо точки О этой оси Oz, не зависит от положения точки на оси.

Иначе: момент силы относительно оси - это алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, взятый отно­сительно точки пересечения оси с плоскостью (рисунок 2.2)

.

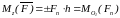Момент силы относительно оси равен нулю, если сила и ось находятся в одной плоскости. Момент силы относительно начала координат 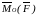равен по (2.1.1)

,

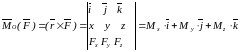откуда получим моменты силы относительно осей координат

, , .

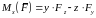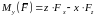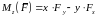П арой сил, приложенной к АТТ, называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рисунок 2.3). Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между ЛД сил пары называют плечом пары, а плоскость, в которой действуют силы пары - плоскостью действия пары. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил.

Действие пары на тело характеризуется моментом пары 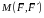, равным ±F∙d, а также положением плоскости действия пары в пространстве и направлением, в котором пара стремится вращать тело, т.о., момент пары сил есть вектор.

Векторный момент пары сил - это вектор 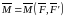, перпендикулярный плоскости действия пары и направленный в ту сторону, откуда видно, что пара стремится повернуть тело против часовой стрелки, и численно равный произведению модуля одной из сил пары на ее плечо. Пару сил можно переносить куда угодно в плоскости и в параллельную плоскость, изменяя модуль силы и плечо пары, но, сохраняя при этом неизменными модуль момента пары и направление, в котором она стремится вращать твердое тело, т.е. пара сил – свободный вектор.

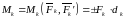
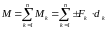
Б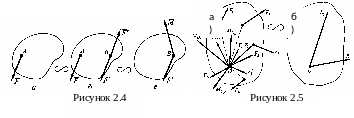 илет3. Приведение системы сил к центру. Теорема о параллельном переносе сил.

Теорема о моменте равнодействующей.

Произвольную систему сил, действующих на АТТ, можно привести к какому-либо центру, заменив все действующие силы одной силой, равной главному вектору системы сил, приложенному в этом центре, и одной парой сил с моментом, равным главному моменту системы сил относительно того же центра (рисунок 2.5)

.

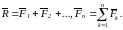
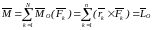При этом 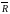не зависит от выбора центра приведения, а 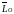– зависит.

Две системы сил, приложенных к АТТ, эквивалентны, если они имеют одинаковые главные векторы и главные моменты относительно одного и того же центра.

Теорема о параллельном переносе силы

Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (рисунок 2.4).

Теорема о моменте равнодействующей.

Теорема Вариньона:

Если система сил, приложенных к абсолютно твердому телу, имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

Векторная запись теоремы: .

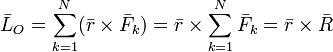Билет4. Плоская система сил. Приведение плоской системы сил к простейшему виду. Равновесие плоской системы сил.

Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что

Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О. В результате останутся следующие три аналитические условия равновесия:

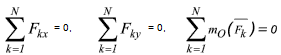
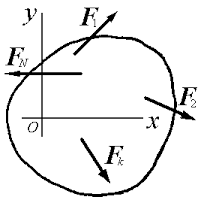
Рисунок 2.

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.

Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил:

                                               R = ΣF_k.

Главным моментом системы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:

                     M_o = ΣM_o(F_k).

Приведение плоской системы сил к простейшему виду.

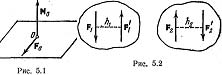
Рассмотрим систему сил (F_1, F₂,..., F_n), расположенных в од­ной плоскости. Совместим с плоскостью расположения сил систему координат Оху и, выбрав ее начало в качестве центра приведения, приведем рассматриваемую систему сил к одной силе F₀=åF_k, (5.1) равной главному вектору, и к паре сил, момент которой равен глав­ному моменту M₀=åM₀(F_k), (5.2) где М_о(F_k)– момент силы F_k относительно центра приведения О. Так как силы распол в одной пл-ти, то сила F_o также лежит в этой плоскости. Момент пары М_о направлен перпенди­кулярно этой плоскости, т.к. сама пара распол в пл-ти действия рассматриваемых сил. Т.о., для плоской сис­темы сил главный вектор и главный момент всегда перпендикулярны друг другу (рис. 5.1). Момент полностью характеризуется алгебраической величиной M_z, равной произведению плеча пары на величину одной из сил, составля­ющих пару, взятой со знаком плюс, если «вращение-» пары происходит, против хода часовой стрелки, и со знаком минус, если оно происходит по ходу часовой стрелки.

Равновесие плоской системы сил

Как известно, необходимыми и достаточными условиями рав­новесия пло­ской произвольной системы сил являются равенства нулю ее главного вектора и главного момента.

Существуют три формы уравнений равновесия плоской систе­мы сил. Пер­вую форму получим, спроектировав на оси координат векторное равенство и присоединив к полу­чившимся двум уравнениям равенство , выражающее условие равенства нулю главного момента:

, , .

 Первые два уравнения называются уравнениями проекций сил на оси координат, третье - уравнением моментов. Точка может быть выбрана произ­вольно.

Легко доказать, что необходимые и достаточные условия равновесия пло­ской системы сил могут быть записаны еще в двух формах.

Вторая форма:  , , ,

 где ось проекций должна быть не перпендикулярна к отрезку

Третья форма: , , ,

где точки не должны лежать на одной прямой.

Отметим, что для любой из трех форм уравнений равновесия число независимых между собой уравнений равновесия равно трем. Задачи, в которых все неизвестные могут быть опреде­лены из уравнений равновесия твердого тела, называются статически оп­реде­ленными. Если же неизвестных больше, чем этих уравнений, то задача оказы­вается статически неопределенной.

Билет5. Трение. Законы трения скольжения. Реакции связей. Угол трения. Трение качения.

Трение в машинах играет существенную роль. В передаточных механизмах — фрикционных, канатных, ременных и др. — передача движения от ведущего звена к ведомому осуществляется трением. В других случаях трение препятствует движению, поглощая значительную часть работы движущих сил.

Законы трения скольжения:

1. Сила трения скольжения прямо пропорциональна силе нормального давления:

Fтр = Ff = f R,

где R — сила нормального давления, направлена перпендикулярно опорной поверхности;

f — коэффициент трения скольжения.

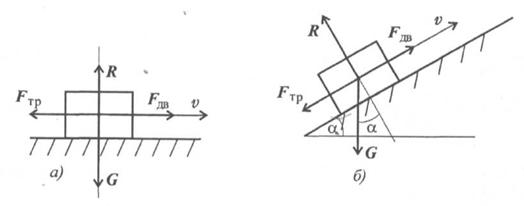
Рис. 13.3

В случае движения тела по наклонной плоскости (рис. 13.3 б))

R = G cos α,

где а — угол наклона плоскости к горизонту.

Сила трения всегда направлена в сторону, обратную направлению движения.

2. Сила трения меняется от нуля до некоторого максимального значения, называемого силой трения покоя (статическое трение):

0 < Ff ≤ Ff0,

где Ff0 — статическая сила трения (сила трения покоя).

3. Сила трения при движении меньше силы трения покоя. Сила трения при движении называется динамической силой трения (Ff):

Ff ≤ Ff0,

Поскольку сила нормального давления, зависящая от веса и направления опорной поверхности, не меняется, то различают статический и динамический коэффициенты трения:

Ff = f R, Ff0 = ff0R.