
- •Тема 1.2. Система автоматического регулирования
- •Вопрос 1. Классификация систем автоматического регулирования
- •Непрерывные системы
- •Дискретные системы
- •Вопрос 2. Состав сар - устройство обратной связи, устройство сравнения, исполнительный механизм, управления
- •Вопрос 3. Управляющее и возмущающее воздействия на объект управления
- •Вопрос 4. Основные показатели качества работы систем автоматического регулирования
- •Вопрос 5. Типовые законы автоматического регулирования
- •Пропорционально-интегральные регуляторы
Пропорционально-интегральные регуляторы
Статическую ошибку, возникающую при пропорциональном регулировании, можно исключить, если кроме пропорционального ввести еще и интегральное звено. Последнее образуется путем постоянного суммирования ε за определенный промежуток времени иформирования сигнала управления, пропорционального полученной величине.
Математически этот процесс может быть описан следующей зависимостью:
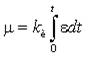 ,
(1.6)
,
(1.6)
где kи=1/Ти – коэффициент пропорциональности интегральной составляющей, а Ти - постоянная времени интегрирования, параметр настройки регулятора.
Если kи ≠ 0, то даже при незначительных отклонениях регулируемой величины сигнал со временем может достичь любой величины, что приведет к перемещению регулирующего органа до момента, пока ε не станет равным 0.
Рассмотрим физический смысл постоянной времени интегрирования. Предположим, что на вход регулятора поступил сигнал ε = εo, а пропорциональная составляющая отсутствует (kп = 0). При этом выходной сигнал в соответствии (1.6) будет меняться по закону μ = εo · t/Tи. По истечении времени t = Tи значение выходного сигнала будет равно μ = ε0 (рис.8, а).
Таким образом, постоянная времени интегрирования в И-регуляторе равна времени, в течение которого с момента поступления на вход регулятора постоянного сигнала сигнал на выходе регулятора достигнет значения, равного значению входного сигнала.
Переходной процесс в И-регуляторе показан на рис.8, б. Устраняя статическую ошибку интегральный регулятор, однако, ухудшает качество переходного процесса. Поэтому на практике применяют комбинированные ПИ-регуляторы.
a |
б |
Рис.8 Закон регулирования (а) и переходной процесс (б) при интегральном (И) регулировании
При этом используется как параллельное соединение пропорционального и интегрального звена (рис.8, а), так и последовательного (рис.8, б).
ПИ-регулятор оказывает воздействие на регулирующий орган пропорционально отклонению и интегралу от отклонения регулируемой величины.
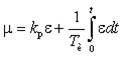 (1.7)
(1.7)
Передаточная функция ПИ-регулятора (по схеме, рис.8, а):
Wпи(р) = kp+ (1.8)
|
|
При скачкообразном изменении регулируемой величины на значение εo ПИ-регулятор со скоростью, определяемой быстродействием привода, перемещает исполнительный механизм на величину (kp · εo), после чего исполнительный механизм дополнительно перемещается в ту же сторону со скоростью εo/Ти, пропорциональной отклонению регулируемой величины. Следовательно, в ПИ-регуляторе при отклонении регулируемой величины от заданного значения мгновенно срабатывает пропорциональная (статическая) составляющая регулятора, а затем постепенно увеличивается интегральная (астатическая) составляющая регулятора.
Переходная характеристика ПИ-регулятора с передаточной функцией (1.8) показана на рис.10 (прямая 1).
Параметрами настойки являются независящие друг от друга коэффициенты усиления kp и постоянная времени интегрирования Ти.
Схема на рис.9, б реализует закон регулирования
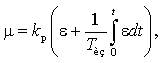 (1.9)
(1.9)
где Тиз – постоянная времени изодрома.
Передаточная функция ПИ-регулятора по схеме рис.9,б:
Wпи(р)
= (1.10)
(1.10)
Таким образом, ПИ-регулятор со структурной схемой, приведенной на рис.9, б, имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту kp. Так, при настройке коэффициента усиления kp будет изменяться и постоянная времени интегрирования:
![]() (1.11)
(1.11)
Рассмотрим физический смысл постоянной времени изодрома Тиз. Предположим, что на вход регулятора поступил постоянный сигнал εo. Тогда выражение (1.9) преобразуется к виду
μ = kp εo(1+t/T) (1.12)


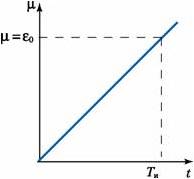

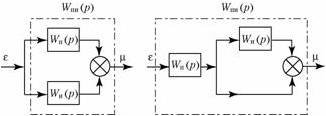 Рис.9.
Структурная схема идеальныхПИ-регуляторов:
а – с передаточной функцией (1.8);б – с
передаточной функцией (1.10)
Рис.9.
Структурная схема идеальныхПИ-регуляторов:
а – с передаточной функцией (1.8);б – с
передаточной функцией (1.10)  Рис.10.
Закон ПИ-регулирования регуляторов
1 – спередаточной функцией (1.8) 2 – с
передаточной функцией (1.10)
Рис.10.
Закон ПИ-регулирования регуляторов
1 – спередаточной функцией (1.8) 2 – с
передаточной функцией (1.10)