Нормальный закон распределения (закон Гаусса).

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности:

*

где параметр μ - математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение (σ² - дисперсия) распределения.

* иногда вместо символа μ будет использоваться символ a.

 Свойства функции f(x):

1. Областью определения функции f(x) является вся числовая ось.

2. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

 4. Функция f{x) имеет в точке х = a  максимум, равный

5°. График функции f(x) симметричен относительно прямой х = а.

6°. Нормальная кривая в точках х = а +s  имеет перегиб,

  

На основании доказанных свойств построим график плотности нормального распределения f(x).

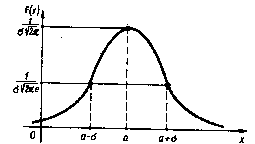
Как видно из рисунка, нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.

При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо.

 

 

 

 

При изменении параметра  s изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение  функции f(x) убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра  кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением s кривая стягивается к прямой х=а.

 

 

 

 

 

Использование формул  f(x) и F(x) для практических расчетов затруднительно. Но решение задач по этим  формулам  можно упростить, если от нормального распределения с произвольными параметрами а и s перейти  к нормальному распределению с параметрами а=0, s = 1.

Функция плотности нормального распределения f(x) с параметрами а=0, s  =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

Функция плотности и интегральная функция стандартной нормальной случайной величины будут иметь вид:

Для вычисления вероятности попадания случайных величин в интервал (a, b) воспользуемся функцией    Лапласа: 

Перейдем к стандартной нормальной случайной величине

     

Тогда

Пример.

Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).

Решение:

 По условию: a  =10, b=50, а=30, s =10, следовательно,

По таблице  находим Ф (2) = 0,4772. Отсюда, искомая вероятность:

Р (10 < Х < 50) =2×0,4772=0,9544.

Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины Х по абсолютной величине меньше заданного положительного числа d, т. е. требуется найти вероятность осуществления неравенства  |x —а|<d.

Заменим это неравенство равносильным ему двойным неравенством

Тогда получим:

Приняв во внимание равенство:

Вероятность заданного отклонения равна

На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d, d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .

Пример. Случайная величина Х распределена нормально. Математическое ожидание и среднее квадратичное отклонение Х соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение: Воспользуемся формулой

  

 По условию ,

тогда

Правило трех сигм

Преобразуем формулу   

     

Введем обозначение

Тогда получим:

  

Если t=3, то

т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратичного отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратичное отклонение, очень мала, а именно равна  0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм:

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратичного отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.