Министерство образования и науки РФ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ШКОЛА ЕСТЕСТВЕННЫХ НАУК

Кафедра экологии

РЕФЕРАТ

по дисциплине «Математические методы в экологии»

на тему «Закон распределения для дискретных и непрерывных случайных величин»

Выполнил студентка гр. Б8313 ___________ С. К. Писцова

Проверил доцент ____________ В. В. Мордухович ____________________________ (зачтено/незачтено)

Г. Владивосток

2013

Достаточно часто на практике рассматриваются такие испытания, в результате реализации которых случайным образом получается некоторое число. Например, при бросании игрального кубика выпадает число очков от 1 до 6, при взятии 6 карт из колоды можно получить от 0 до 4 тузов. За определенный промежуток времени (день, месяц) в городе регистрируется то или иное количество преступлений, происходит какое-то количество дорожно-транспортных происшествий.

Во всех перечисленных испытаниях мы сталкиваемся с так называемыми случайными величинами.

Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.

Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной (дискретно распределенной).

Непрерывной случайной величиной называется такая случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Для задания случайной величины недостаточно перечислить ее всевозможные значения. Иногда величины могут принимать одни и те же значения. Но вероятности, с которыми эти случайные величины принимают свои значения, будут совершенно разными. Поэтому для задания дискретной случайной величины кроме перечня ее всех возможных значений нужно еще указать их вероятности.

Соответствие между возможными значениями случайной величины и их вероятностями называют законом распределения дискретной случайной величины.

Закон распределения можно задать в виде таблицы, формулы или графически.

При табличном задании закона распределения в первой строке таблицы записываются возможные значения случайной величины, а во второй – соответствующие значениям вероятности:

X	x1	x2	…	xn
P	p1	p2	…	pn

Такая таблица называется рядом распределения дискретной случайной величины X. Так как случайная величина в результате испытаний имеет только одно значение, то сумма вероятностей этих событий равна 1.

+ +…+ = =1

Для наглядности ряд распределения случайной величины можно изобразить в виде графика.

Распределение дискретных случайных величин

Биномиальный закон распределения.

Биномиальным называется распределение вероятностей, определяемое формулой Бернулли:

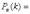
- формула является аналитическим выражением биномиального закона распределения, где p – вероятность появления события, 0<p<1; q – вероятность противоположного события, q=1–p; C – биномиальный коэффициент.

По биномиальному закону распределена случайная величина Х числа появлений события А при проведении n независимых испытаний, если вероятность появления события А в каждом испытании одинакова и равна p. В n испытаниях событие А может вообще не появиться, появиться 1 раз, 2 раза, …, n раз. Таким образом, возможные значения Х таковы: =0, =1, =2, =3, …, =n. А соответствующие им вероятности подсчитываются по формуле Бернулли. Ряд распределения в этом случае будет таким:

X	0	1	2	…	n
P	qn			…	pn

Cсумма вероятностей, соответствующих возможным значениям случайной величины, записывается в виде бинома Ньютона:

+ + +…+ +…+ = = .

Пример.

Какова вероятность появления 0, 1, 2, 3, 4, 5 самцов в числе пяти новорождённых львят?

Возможна серия из пяти повторных наблюдений с двумя исходами. Но при этом ^{появление} самцов может быть различно (от 0 до 5). В каждом из пяти испытаний вероятность события A(p) или A(q) будет одинаковой и равна 0,5. Вероятность того, что не будет ни одной особи мужского пола, составит P₅(0)=5!/0!×5!×(0,5)⁰×(0,5)⁵=0,03125. Так же можно рассчитать вероятность появления одного самца, двух, трёх, четырёх, пяти. Если просуммировать все вероятности мы получим единицу.