
- •1. Магнитное поле. Вектор магнитной индукции, линии магнитной индукции. Поток вектора магнитной индукции. Теорема Гаусса.
- •2. Движение заряженных частиц в магнитном и электрическом полях.
- •3.Теорема о циркуляции вектора магнитной индукции для поля в вакууме. Магнитное поле соленоида и тороида (с выводом).
- •8. Явление самоиндукции. Эдс самоиндукции. Индуктивность проводящего контура. Индуктивность длинного прямого соленоида (с выводом).
- •Индуктивность соленоида
- •11)Магнитная энергия тока. Плотность энергии магнитного поля
- •12. Фарадеевская и максвелловская трактовки явления электромагнитной индукции.
- •13. Ток смещения
- •Током смещения сквозь произвольную замкнутую поверхность s называется физическая величина, равная потоку вектора плотности тока смещения сквозь эту поверхность
- •16) Относительность электрических и магнитных полей.
Второе уравнение Максвелла основано на предположении, что всякое изменение электрического поля вызывает возникновение в окружающем пространстве вихревого магнитного поля.
Количественной мерой магнитного действия переменного электрического поля является ток смещения.
Током смещения сквозь произвольную замкнутую поверхность s называется физическая величина, равная потоку вектора плотности тока смещения сквозь эту поверхность
![]() с
плотностью тока смещения
с
плотностью тока смещения
![]() где D –
вектор электрического смещения.
где D –
вектор электрического смещения.
Токи смещения проходят по тем участкам цепи переменного тока, где отсутствуют проводники (например, между обкладок конденсатора).
В диэлектрике вектор электрического смещения равен
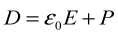 где
Р – вектор поляризованности.
Тогда
плотность тока смещения
где
Р – вектор поляризованности.
Тогда
плотность тока смещения
 где
где  –
плотность тока смещения в вакууме,
а
–
плотность тока смещения в вакууме,
а 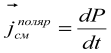 –
плотность тока поляризации (смещение
зарядов в молекулах неполярных
диэлектриков или поворот диполей
полярных диэлектриков).
–
плотность тока поляризации (смещение
зарядов в молекулах неполярных
диэлектриков или поворот диполей
полярных диэлектриков).
Токи смещения не сопровождаются выделением теплоты.
Второе уравнение Максвелла в интегральной форме имеет вид

По теореме Стокса
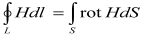 а
полный ток
а
полный ток
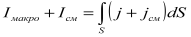 вследствие
чего в
дифференциальном виде второе уравнение
Максвелла имеет
вид
вследствие
чего в
дифференциальном виде второе уравнение
Максвелла имеет
вид
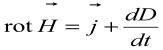
14. Полная система уравнений Максвелла в интегральной форме.
Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле может быть как потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ+ЕB. Так как циркуляция вектора ЕQ равна нулю , а циркуляция вектора ЕB определяется выражением, то циркуляция вектора напряженности суммарного поля:

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н:

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D:

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то эта формула запишется в виде:

4. Теорема Гаусса для поля В:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):



Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
15)
Система уравнений Максвелла : диффер. форма. Материальные уравнения.
Теорией Максвелла назвывается последовательная теория единого электромагнитного поля, создаваемого произвольной системой электрических зарядов и токов. В теории Максвелла решается основная задача электродинамики :заданному распределению зарядов и токов отыскиваются характеристики создаваемых ими электрического и магнитного полей. Если мы из системы 4-х уравнений перейдем в проэкции на оси ( E - Ex Ey Ez, B - Bx By Bz), то не сможем решить ее, из-за большого кол-ва неизвестных. Для их нахождения пользуются так называемыми материальными уравнениями, характеризующими электрические и магнитные св-ва среды.
Анализ уравнений Максвелла. 1-е уравнение указывает на то, что поле является вихревым (вопр. 30). 2-е уравнение - Максвелл обобщил теорему Остроградского-Гаусса для электростатического поля. Он предположил, что она справедлива для любого электрического поля как стационарного, так и переменного. 3-е уравнение : См. ток смещения. В интегральной форме показывает, что циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур. 4-е уравнение - теорема Остроградского-Гаусса справедлива для любого магнитного поля.
Если электрические и магнитные поля стационарны (dD/dt = dB/dt = 0), то эти поля существуют независимо друг от друга. Электрическое поле описывается двумя уравнениями электростатики : rot E = 0 и div D
