1. Магнитное поле. Вектор магнитной индукции, линии магнитной индукции. Поток вектора магнитной индукции. Теорема Гаусса.

Магнитное поле и его характеристики. При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34).Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле  распространяется со скоростью света, т. е. 300 000 км/с.

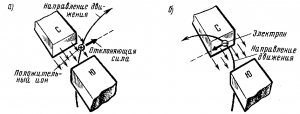
Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б).

Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.

Направление этого вектора для поля прямого проводника с током и соленоида можно определить по пра­вилу буравчика: если направление поступательного движения буравчика (винта с правой нарезкой) совпадает с направлением тока, то направление вращения ручки буравчика покажет направление линий магнитной индукции. Вектор магнитной индукции направлен по касательной к линиям.

Линии магнитной индукции. Это линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции. Силовые линии магнитного поля всегда замкнуты. Их направление определяется правилом « правой руки» или правилом буравчика.

Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:

Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)

Магнитный поток - величина скалярная.

Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность.

Теорема Гаусса для магнитной индукции:

Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:

2. Движение заряженных частиц в магнитном и электрическом полях.

Электрические и магнитные поля действуют на движущиеся заряженные частицы с известной силой. Поэтому эти поля могут использоваться для управления движением заряженных частиц. Потоки движущихся заряженных частиц широко используются в различных приборах, принципы действия и применения некоторых из них мы рассмотрим в данном параграфе.  Описание движения заряженной частицы проводится на основании второго закона Ньютона, уравнение которого имеет вид

где qE − сила, действующая на частицу с электрическим зарядом q со стороны электрического поля; qv x B − сила Лоренца, действующая на частицу со стороны магнитного поля. В общем случае напряженность электрического поля E и индукция магнитного поля B могут зависеть от координат (в неоднородных полях) и времени (в нестационарных полях). Для однозначного решения уравнения (1) его необходимо дополнить начальными условиями: положением частицы r_o и скоростью v_o в некоторый момент времени t_o.  При описании распространения потоков частиц в некоторых случаях необходимо также учитывать взаимодействия частиц между собой, или принимать во внимание зависимость характеристик полей от положения и скоростей других частиц. Наконец, при записи уравнения (1) принято, что частицы движутся в вакууме, где отсутствуют силы сопротивления среды. Движение частиц в средах, обладающих сопротивлением, описываются в рамках уравнений для электрического тока. При движении частиц в электромагнитном поле, как правило, пренебрегают действием силы тяжести, которая обычно значительно меньше электромагнитных сил.  Записанное уравнение движения справедливо для частиц, движущихся со скоростями, значительно меньшими скорости света. В противном случае необходимо использовать релятивистские уравнения движения теории относительности.  Рассмотрим некоторые частные простейшие случаи решения уравнения (1) для частиц, движущихся в стационарных полях