Расчётно-графическая работа Структурный, кинематический и силовой анализы плоского рычажного механизма
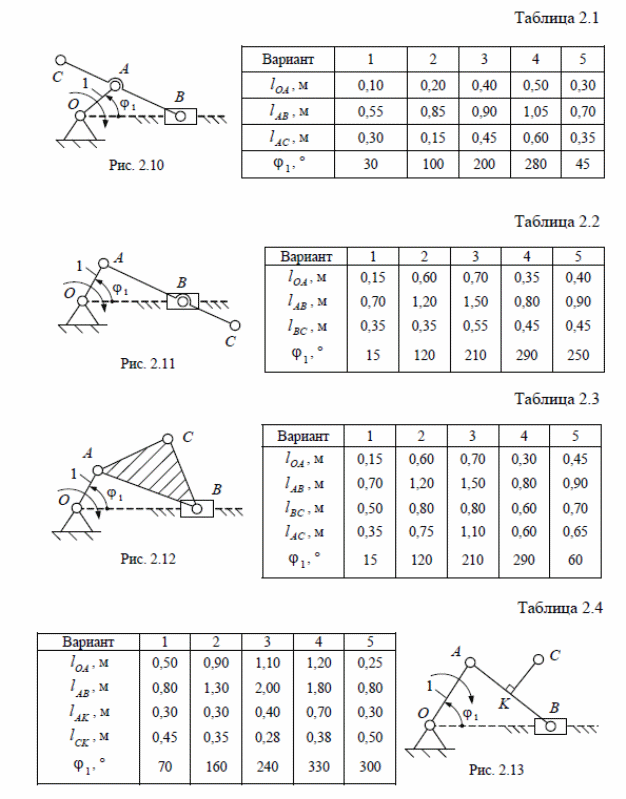
По исходным данным и заданной схеме (рис. 1):
провести структурный анализ механизма;
построить положения механизма в 8 точках положения кривошипа;
построить заданное углом φ1 положение механизма, для которого, используя графоаналитический метод (метод планов), определить линейные скорость и ускорения точек звеньев и угловые скорости и ускорения звеньев механизма;
указать на схеме механизма направление угловых скоростей и ускорений.
Пример выполнения
Выполнить структурный, кинематический и силовой анализы плоского четырёхзвенного рычажного механизма.
Исходные
данные: схема механизма и его кинематические
размеры:
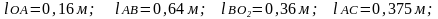
Входное звено AO1 вращается с постоянной угловой скоростью n1 = 500 об/м-1 . Исследование провести для положения механизма, определяемого углом φ1=40 0.
1.Структурный анализ механизма
Степень подвижности механизма определяем по формуле Чебышева:
,
где n=3 – число подвижных звеньев, p5 =4 – число кинематических пар пятого класса, p4 =0 – число кинематических пар четвёртого класса
.
Формула строения данного механизма имеет вид:
Т.е. к исходному механизму, стоящему из стойки 0 и входного звена 1 присоединена структурная группа 2,3 второго класса второго порядка. Таким образом, рассматриваемый механизм является механизмом второго класса.
2. Кинематический анализ механизма
Построение положений механизма (рис. 2)
Выбираем масштабный коэффициент длины для схемы:
По значениям X и Y определяем взаимное расположение кинематических пар O1 и O2 в масштабе µl.
,
.
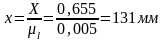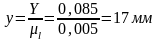Проводим из центра O2 дугу радиусом
затем на ней из точки O1 делаем две засечки радиусами
Рис. 2. Графические построения
Отметим точки B0 и B6 .
Траектория точки А – окружность радиуса
Соединив точки B0 и O1 и продлив линию до пересечения с траекторией точки А, получим положение точки А0 в левом крайнем положении; соединив точку B0 с O2, получим положение коромысла B0O2 в левом крайнем положении. Таким образом, положение O1А0B0O2 - левое крайнее положение механизма. После соединения точек O1 и B6
Получим точку A6, которая определит положения кривошипа, шатуна и коромысла в крайнем правом положении механизма – O1А6B6O2.
Приняв левое крайнее положение механизма за нулевое, разбиваем траекторию точки A на 12 частей, определяем 12 положений точки A, затем, методом засечек находим соответствующие положения точек B, С, S2. Нумерацию положений механизма ведём в направлении угловой скорости (указано дуговой стрелкой) входного звена 1. Определив 12 положений точки S2 и, соединив их плавной кривой, получаем траекторию точки S2 - шатунную кривую точки S2.
Строим заданное положение механизма, определяемое углом φ1=400. Обводим его жирной линией.
4. Определение линейных скоростей точек звеньев и угловых скоростей звеньев
Угловая скорость кривошипа OA
.
Скорость
точки A
Для определения скорости точки B запишем векторные уравнения скоростей:
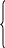
где
,
.
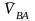
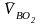
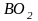В
этой системе векторных уравнений
известны:VA
по величине и направлению (перпендикулярна
AО1),
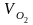=0.
Решаем систему уравнений графическим методом (методом планов скоростей), для чего выбираем масштабный коэффициент плана скоростей:
.
Из полюса pV плана скоростей откладываем в направлении скорости VA отрезок pV a
= 83,7 мм, через точку a проводим прямую перпендикулярную к AB.
В соответствии со вторым уравнением системы через точку O2 (точка O2 совпадает с полюсом pV, т.к. =0) проводим прямую перпендикулярно BO2. Точка пересечения перпендикуляров определяет положение точки b – конца вектора скорости VB. Соединяя точку b с полюсом pV , получим отрезок pV b, который в масштабе µV определяет скорость точки B:
.
Для определения скорости точки S2 воспользуемся свойством плана скоростей, согласно которому векторы относительных скоростей точек звена образуют на плане скоростей фигуру, подобную фигуре, образованной этими же точками на плане звена и повернутую относительно неё на 90° в направлении угловой скорости звена.
Из плана скоростей находим:
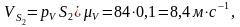
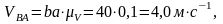
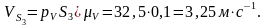
Угловые скорости звеньев:
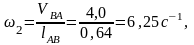
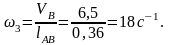
Направление угловых скоростей ω2 и ω3 определяются соответственно направлениям линейных скоростей VBA и VB .