
Решение задач
Энтропия
Цель занятия: на конкретных примерах усвоить основные понятия теории информации и энтропии.
Расчетные формулы
Количество
информации
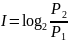 ,бит (1)
,бит (1)
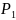 -
априорная вероятность, являющаяся
мерой неопределенности, знаний о событии
до получения сообщения ;
-
априорная вероятность, являющаяся
мерой неопределенности, знаний о событии
до получения сообщения ;
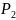 - апостериорная вероятность ,
являющаяся мерой знаний о событии после
получения сообщения
- апостериорная вероятность ,
являющаяся мерой знаний о событии после
получения сообщения
При =1 (безошибочный прием сообщения ) выражение примет вид
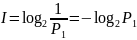 (2)
(2)
определяет собственное количество информации в сообщении.
Если алфавит
дискретного сообщения имеет n
– символов, то его можно рассматривать
как случайную величину Х, возможными
значениями которой являются используемые
в алфавите символы х1,х2,х3, хn
с известными вероятностями
появления их в тексте,Р(х1) =
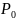 . Среднее количество собственной
информации, приходящейся на один символ
из множества всех символов данного
алфавита, называется энтропией дискретного
сообщения (случайной величины Х)
. Среднее количество собственной
информации, приходящейся на один символ
из множества всех символов данного
алфавита, называется энтропией дискретного
сообщения (случайной величины Х)
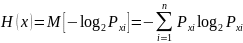 бит /символ.
бит /символ.
Энтропия характеризует степень неопределенности случайной величины Х Энтропия на выходе дискретного канала связи определяется как среднее количество информации, прошедшее по каналу связи с одним символом.
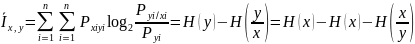
Где
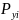 – вероятность появления символа
– вероятность появления символа
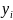 на выходе канала связи
на выходе канала связи
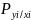 - вероятность появления на выходе канала
связи символа
-, при условии появления
- вероятность появления на выходе канала
связи символа
-, при условии появления
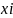 на выходе
на выходе
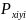 - вероятность одновременного появления
символов
- вероятность одновременного появления
символов
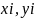 на входе и выходе канала связи,
соответственно.
на входе и выходе канала связи,
соответственно.
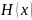 - энтропия сообщения на входе ;
- энтропия сообщения на входе ;
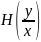 и
и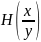 -
условные энтропии, характеризующие
воздействие помех.
-
условные энтропии, характеризующие
воздействие помех.
Пропускная способность канала связи С может быть определена по формуле:
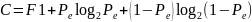
F
– полоса пропускания канала;
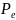 - вероятность искажения сообщения.
- вероятность искажения сообщения.
Решения задач
Задача 1.Самолет противника с равной вероятностью может находится в одной из 250 зон. Какое количество информации будет получено при обнаружении самолета в одной из зон, если вероятность правильного обнаружения равна 0,9846.
Решение
Выбор расчетной формулы
Определение
Априорная
вероятность появления самолета в одной
из зон находится с использованием
классического определения вероятности
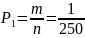 = 0.0004
= 0.0004
Определим . при обнаружении самолета в одной из зон, правильность такого решения можно гарантировать с вероятностью 0,9846. Следовательно = 0,9846.
Определение
количества информации
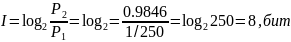
Ответ : I = 8 , бит,
Задача 2:
Известно, что энтропия русского текста
составляет приблизительно 0,5
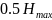 .Какое количество информации получит
читатель, прочтя произвольное слово из
6- ти букв.
.Какое количество информации получит
читатель, прочтя произвольное слово из
6- ти букв.
Решение
1. Определяем
максимальную энтропию одной буквы.
Машинописный алфавит русского текста
содержит 32 буквы. Энтропия максимальна,
если все символы используемого алфавита
равновероятны. Следовательно, для
алфавита , объема
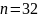
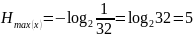 бит/ симв.
бит/ симв.
2. Определение количества информации в слове. в случае слова из m- = 6 , букв.
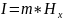 по условию
по условию
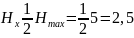 ,бит / симв.
,бит / симв.
Тогда
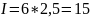 , бит
, бит
Ответ: 15 бит.
Задача:
Определить пропускную способность
двоичного симметричного канала связи
с полосой пропускания
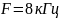 и вероятностью ошибочного приема
символа из – за помех
и вероятностью ошибочного приема
символа из – за помех
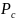 = 0.3/
= 0.3/
Решение:
Выбор исходной формулы
Ответ :
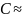 950 бит / сим.
950 бит / сим.
Задача 4. Для
передачи сообщения, используется
алфавит объема
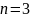 Вероятности
Вероятности
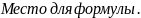 появления
символов этого алфавита в сообщении
появления
символов этого алфавита в сообщении
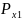 =
=
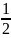 ;
;
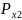 =
=
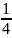 ;
;
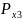 =
. При передаче по каналу связи символы
могут быть искажены с одинаковой
вероятностью
=0,1.
Определить средне количество информации
на выходе такого канала связи .
=
. При передаче по каналу связи символы
могут быть искажены с одинаковой
вероятностью
=0,1.
Определить средне количество информации
на выходе такого канала связи .
