• Неустойчивое :  Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему.

• Устойчивое равновесие : Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия.

• Безразличное равновесие : Если система будет смещена на небольшое расстояние, она останется в новом положении.

21.2 Условия : Механическое равновесие - состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой оси вращения равна нулю.

22. Момент и плечо силы. Пара сил.

М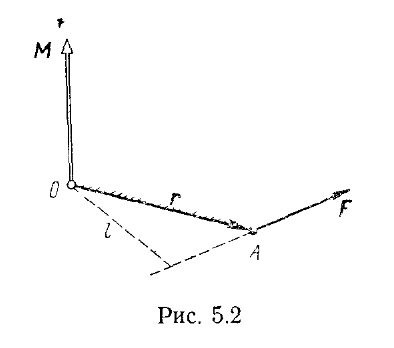 оментом силы F относительно точки О называется векотор ,равный веторному призведению векторов и . =[ , ]

- аксиальный вектор.

Модуль : | M | = l . F

Где : l – Плето силы относительно точки О.

Уравнение моментов : =

где - момент импульса.

L=lp=lmv

Где : l – Плето силы относительно точки О.

Пара силы

Две равные паралельные силы F₁ и F₂ , направленных в противоположные стороны, такие силы образуют пару сил.

23. Момент импульса. Момент импулься механической системы.

М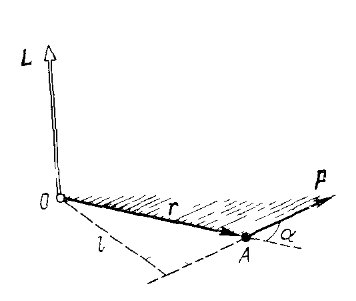 омент импульса тела относительно точки О называют , равный векторному произведению векторов и .

= [ , ]

- аксиальный вектор

Модуль L = rp sin = lp

Где : l-плечо вектора относительно точки О.

Момент импульса системы

= - Момент импульса L равен сумме моментов импульсов частей L_i

24. Теорема об изменении момента импульса системы. Закон сохранения момента импульса системы. Момент импульса относительно оси. Момент импульса относительно подвижного начала и подвижной оси.

24.1 Теорема об изменении момента импульса системы

Изменение момент импульса системы - =

– величина аддитивная - Момент импульса системы равен сумму моментов импульсов отдельных частей _i

По времени : = = +

Где - суммарный момент внутренних сил относительно точки О

- суммарный момент внешних сил относительно точки О

Относительно любой точки = 0 → = → L₂ – L₁ =

(производная момента импульса системы по времени равна сумме моментов всех внешних сил)

24.2 закон сохранения момента импульса системы

Момент импульса замкнутой системы остается постоянным

L = = const

З акон сохранения момента импульса имеет место только по отношению к инерциальным системам отсчёта.

Прирыщение момента импульса одной части равно убыли момента импульса другой части.

24.3 Момент и импульса относительно оси

Моментом импульса относительно оси z называют проекцию на эту ось. , определунного относительно произвольной точки О данной оси = M_Z

Производная по времени от момента импульса частицы относительно оси z равно моменту силы относительно этой оси.

Если M_Z = 0,то L_Z = const

24.4 Момент импульса относительно подвижного начала и подвижной оси

= = + → = +

Где М – суммарный момент сил относительно О

М’ – суммарный момент сил относительно О’

F= - внешние силы

25. Связь момента импульса с угловой скоростью. Кинетическая энергия при вращательном движении. Работа, совершаемая моментом силы.