16. Механическая работа. Работа переменной силы. Мощность.
1
6.1
Механическая работа
: действие силы F
на перемещении dr
харакризуют Fdr
δA = F.dr – элементарная работа – величина, равная скалярному произвидению силы, действующей на тело, на его перемещение.
16.2 Работа переменной силы
A
= 
= 
или 
+ Работа упругой силы
F = -æ.r , r – радиус-вектор частиц M относительно точки О
δА = F.dr = -æ.r.dr
A
= - 
= 
- 
+Работа гравитационноий силы
F
= 
. lr
, lr
– орт радиус-вектора r
δA = F.dr = . lr. dr
A
= 
= 
- 
+ Работа однородной силы тяжести
F = -mgk , k – орт вертикальной оси z
δA = F.dr = -mgk.dr → A = mg (z1 – z2)
16.3 Мощность :
Для
характеристики скорости, с которой
совершается работа вводят величину,
называемую мощностью. N
= 
= F.v
(ватт - Вт) 
17. Энергия. Теорема об изменении кинетической энергии системы. Теорема Кенига.
17.1 Энергия
Энерния является мерой способности физической системы совершить работу. эту величину – сумму кинетической и потенциальной энергий – называют полной механической энергией частицы в поле и обозначают E.
E = K + U
K – потенциальная энергия
U – кинетическая энергия
17.2 Теорема об изменении кинетической энергии системы.
Приращение
кинетической энергии частицы на некотором
перемешении равно алгебратической
сумме работ всех сторонных сил, действующих
на частицу на том же перемещении.
T2 – T1 = Aстор
Aстор > 0 – полная механическая энергия частицы увеличивается
Aстор < 0 – полная механическая энергия частицы уменьшается
17.2 Теорема Кёнига :
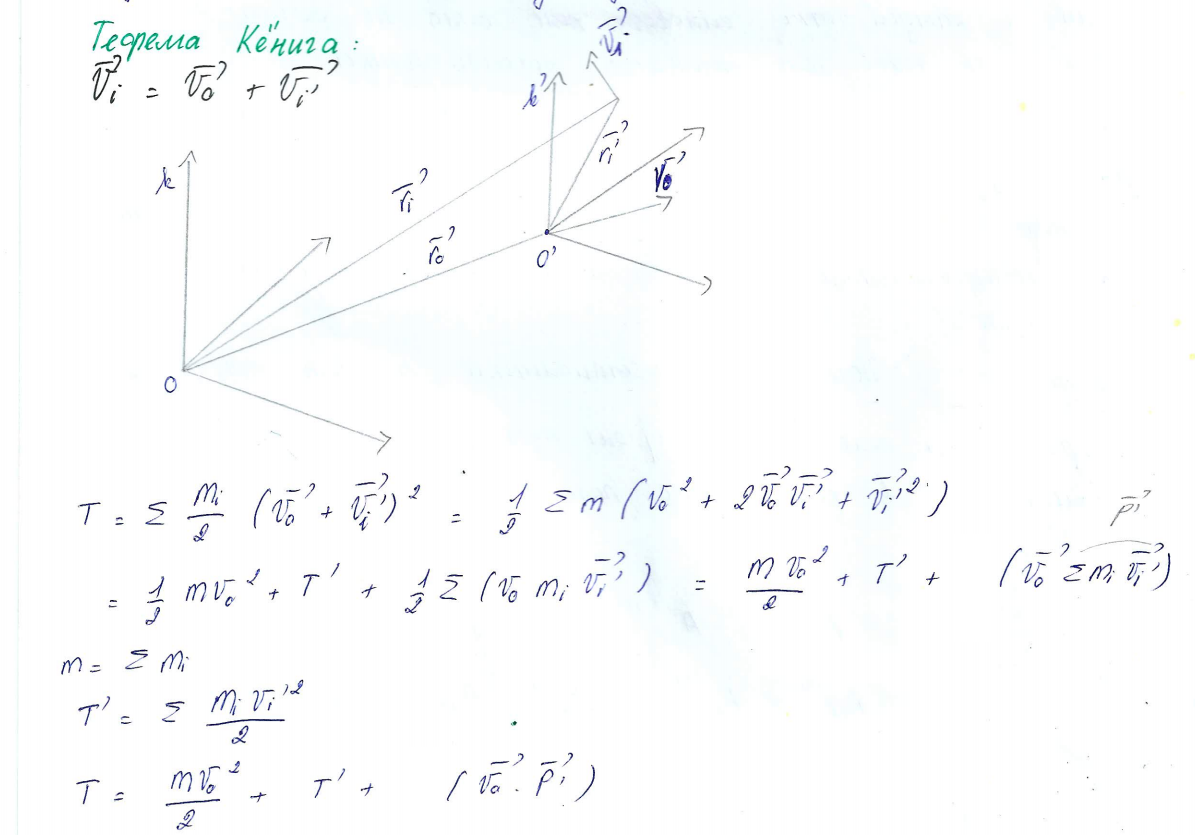
Ц – система система отчета, жестко связанная с центром масс и перемащаюсь поступательно по отнощению к инерциальным системам, называют системой центра масс (Ц – системой )
Ц – система обладает особеностью, что полный импульс системы частиц в ней всегда = 0
18. Потенциальное поле сил. Потенциальна энергия взаимодействия.
18.1 Потенциальное поле сил :
Полем сил называтеся область пространства, в каждой точке которого сила, которая действует на помещенную туда частицу, меняется законмерно от точки к точке.
Если в кажой точке силового поля сила не зависит от времени, то такое поле называется стационарным .
Стациональное силовое поле, в котором работа силы поле на пути между 2-мя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным полем. И сами эти силы называются консервативными.
18.2 Потенциальная энергия взаимодействия.
Возьём систему из двух чатиц :
Пусть в некоторой системе отсчёта в момент времени t, положение.
Частиц
определяется – вектора 
и 
за время dt
частицы совершают перемещения d
и d
, то работа сил взаймодействия 
и 
δA1,2 = ( . d ) + ( . d )
Согласно третьему закону Ньютона = -
δA1,2 = ( . d ) - ( . d ) = (d - d )
= 
-
, dr12
= d
- d
→ δA12
=
. d
+ Для центральных сил работа сил поля равна убыли потенциальной энергии
δA12 = - dU12
Возьём систему из трёх частицы
δA = δA12 + δA13 + δA23 = - (dU12 + dU13 + dU23 )
то для ситемы из множества частиц : δA = -dUin
U – сооветвенная потенциальная энергия данной системы частиц полученной результат можно общить на произвольное число частиц каждой конфигирации произвольной системы частиц присища собственная потенциальная энергия.
U и работа всех внутренных центральных сил при изменении этой конфигурации равна убыли собственной потенциальной энергии системы.
δA = -dU , ∆U = U1 – U2
19. внутреняя энергия
Внутреняя энергия системы - это сумма всех кинетической энергии всех частиц, из которорых состоит ситема, и потециальной энергии их взаймодействия между частями.
20. Теорема об изменении полной механической энергии системы. Закон сохранения энергии в механике.
20.1 Теорема : Прирещение полной механической энергии частицы на некотором пути равно алгебраической сумме робот всех сторонних сил, действующих на частицу на том же пути
E2
– E1
= Aстор
Aстор > 0 – польная энергия частицы увеличивается
Aстор < 0 – польная энергия частицы уменьшается
20.2 Закон сохранения энергии в механике:
Если сторонние силы отсутствуют или таковы, что не совершают работы в течение интересующего нас времени, то польная мезаническая энергия частицы в стационарном поле консервативаных сил остается постоянной за это время. E = K + U = const
21. Равновесные состояния. Условия равновесия механической системы.
21.1 Равновесные состояния
Это состояние , в котором тело находится в покое или движется равномерно прямолинейно или вращается без касательного ускорения.
Виды равновесия: