1/ Система отчёта, перемещение . Скорость.Средняя и мгновенная скорости. Путь. Средняя путевая скорость. Ускорение.

1.1 Система отчёта

Положение тела в пространстве может быть определенно только по отношению к каким-либо другим телам. Это относится к движению тела, к изменению его положения с терчением времени.

Тело , которое служит для определения положения интересующего нас тела, называют телом отсчёта.

Совокупность тела отсчёта и связанных с ним кординат и синхронизированних между соббой часов образует систему отсчёта.

1 .2 перемещение

Описание движения при помощи расстояний и промежутков времени возможно только тогда, когда выбрана определенная система отсчёта.

Вектор перемещения ∆r представляет собой приращение радиуса вектора за время ∆t , т.е вектор, проведенный изначального положения в конечное.

1.3 Скорость.Средняя и мгновенная скорости

Отношение называют средним вектором скорости за время ∆t.

Вектор <v> совпадает по направлению с ∆ . < > = .

Мгновеная скорость : V = =

Определим вектор скорости точки в данный момент как придел отношения при ∆t 0 :

Вектор скорости в данный момент ( мгновенная скорость) равен производной от радиуса-вектора r по времени и направлен по касательной к троектории в данной точке в сторону движения точки.

1.4 Путь - это длинна участка траектории, пройденного материальной точкой.

1.5 Средняя путевая скорость : <v> =

Это средняя скорость по перемещению, которая будет вектором, равным отношению перемещении к времени, за которое он совершено. Cреднюю путевую скорость определяют таким образом, может равняться 0 даже тело движилось .

1.6 Ускорение

Ускорение : движение точки характеризуется также ускорением. Вектор ускорения определяет скорость изменеия вектора скорости со времением : =

То есть ускорение равно производной от вектора скорости по времени. Направление вектора а совпадает с направлением вектора .

2.Закон движения и Уравнение троектории :

2.1 Закон движения : Запишем проекции на Оx, Oy, Oz радиуса-вектора r(t) характеризующего положения интересующей нас точки относительно тачала координат О в момент t:

x = x(t) , y = y(t) , z = z(t) и получается r = r(t) = x(t).i + y(t).j + z(t).k

Зная зависимость этих координат от времени – закон движения точки, можно найти положения точки в каждый момент, её скорость и ускорение.

2.2 Уравнение траектории: это зависимость (математическая формула) некоторой кординаты от другой, без времени. Оно показывает как движется тело и какую траекторию совершило движения. Y=f(x)

3. Cпособы задания движения. Проекции ускорения в прямоугольной и естественной системе координат.

3.1 Векторный способ

В этом способе положение интересующей нас точки А задают радиусом – вектором r , проведенным из некоторой неподвижной точки О выбранной системы отсчёта в точку .

При движении точка и её радиус-вектор меняются в обюем случае как по модулю, так и по направлению, то есть радиус-вектор r зависит от времени t.

Геометрическое место концов радиуса-вектора r называют траекторией.

3.2 Координатный способ :

В этом способе с выбранным телом отсчёта жестко связывают определеную систему координат (чаще всего это декартову).

Запишем проекции на Оx, Oy, Oz радиуса-вектора r(t) характеризующего положения интересующей нас точки относительно тачала координат О в момент t:

x = x(t) , y = y(t) , z = z(t)

Зная зависимость этих координат от времени – закон движения точки, можно найти положения точки в каждый момент, её скорость и ускорение.

r = x(t).i + y(t).j + z(t).k   v = i + j + k  a = i + j + k

по муделю a =

то есть проекции ускорения в прямоуголной системе кординат.

3.3 Естественный способ

Этот способ принимают тогда, когда троектория точки известна заранее. Положение точки А определяют дуговой кординатной l – расстоянием в доль траектории от выбранного начала отсчёта О.

В ведем единичний вектор т , связанный с движущейся А и направленный по касательной к троекторий в сторону возрастания дуговой кординаты l. То получим:

= v_т =

Ускорение

= = = . + . = . + v_т . . = . + .

= . + . = a_{т +} а_n

a_т - тангенциальное ускорение , а_n – нормальное ускорение

то есть ускорение в естестсвенной системе

4. Принцип относительности Галилея. Преобразования Галилея.

Принцип относительности Галилея для инерциальных согладно что, все инерциальные системы по своим механическим свойствам эквивалентны друг другу.

Это значит во всех инерциальных системах отсчёта свойства времени и пространства одинаковы, одинаковы а также законы механики.

Преобразавания Галилея при переходе от одной инерциальной системы отсчета к другой. Пусть инерциальная система К’ движется со скоростью V относительно другой инерциальной системы K.

5. Первый закон Ньютона. Инерциальные системы отсчёта – первый закон (закон инерции)

5.1 Первый закон Ньютона

Существуют такие системы, называемые инерциальными, относительно которых метериальная точка при отсутствии внешних воздействий сохраняет величину и направление скорости неограниченно долго.

5.2 Инерциальные системы отсчёта

Существует такая система отсчета, в которой ускорение материальной точки целиком обуссловлено только взаймодействием с другими телами. Свободная материальная точка, неподверженная действию никаких других тел, движется относительно такой системы отсчета прямолинейно и равномерно, или как говорят по инерции. Такую систему называют инерциальной.

6. Масса и импульс тела. Второй закон Ньютона

6.1 Масса :

• Всякое тело « отказывает » сопротивление при любых попытах изменить его скорость – как по модулю, так и по направлению. Это свойство, называют инертностью.

• Мерой инертности служит величина, называемая массой.

Свойства:

Масса – величина аддитивная, то есть масса составного тела равна сумме масс его частей.

Масса – величина постояная, то есть не изменяется при его движении.

6.2 Второй закон Ньютона :

Произвидение массы материальной точки на её ускорение равно действующей на неё силе : ma = F

Уравнение движения материальной точки.

Однако, у нас есть : m = F ↔ = F ( масса постояная)

↔ = F ( = m. )

= m. ,эта величина называется импульсом материальной точки.

6.3 импульс тела : это количество движения

7. Силы в природе. Принчип супрепозиции сил. Классификация сил.

7.1 Силы в природе

• Сила – это векторная величина , харатеризующая интенсивностью взаймодействия тел.

7.2 Принцип суперпозиции сил

« На всякую материальную точки в данных конкретных условиях действует, строго говоря, всего только одна сили F» .

7.3 Классификация сил

8. Сила тяжести и вес. Упругие силы. Силы трения.

8.1 Сила тяжести

8.2 Вес 

• сила воздействия тела на опору, препятствующую падению, возникающая в поле сил тяжести.

• Вес P тела, покоящегося в инерциальной системе отсчёта  , совпадает с силой тяжести, действующей на тело.

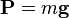
8.3 упругие силы.

При деформации тела возникает сила, противодействующая этой деформации. Эта сила называется силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия.

8.4 Силы трения

• Сила трения покоя - возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения.

Максимальная сила трения покоя в простейшем приближении:  , где k₀ —коэффициент трения покоя, N — сила нормальной реакции опоры.

• Сила трения скольжения

• Сила трения катения

• Сила сопротивление : F = -kv , в газе или в жидкости

1. Сила гравитационного притяжения, действующая между двумя материальными точками.

F = .

Где – гравитационая постояная

2. Кулоновская сила, действующая между 2 точечными зарядами :

F = k.

3. Однородная сила тяжести : F = mg

4. Упругая сила : F = -kr , r-смещение

5. Сила трения скольжения, возникающая при скольжении вонного тела по поверхности другого тела: F = -k R_n­

k- констант треня скольжения , R_n – сила нормального давления

6. Сила сопротивление : F = -kv , в газе или в жидкости

Сили гравитационного притяжения, действующая между двумя материальными точками.

F = . , - гравитационная постояная

9. Третий закон Ньютона. Пределы применимости классической механики.

9.1 Третий закон Ньютона :

Силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в протовополодные стороны вдоль прямой, соединяющей эти точки : F₁₂ = - F₂₁ .

9.2 Пределы:

Три типа симуаций, в которых классическая механика не выполняется.

1. При очень маленьких размерах или массах. -  квантовая механика

2. При скоростях, близких к скорости света. - специальная теория относительности

3. При рассмотреним системы с очень большим числом чатиц. ( или же большим числом стененей свободы ). - статистическая физика.

10. Полный механический импульс. Теорема об изменеии импульса системы.

10.1 Полный механический импульс

Уравнение движения материальной точки.

Однако, у нас есть : m = F ↔ = F ( масса постояная) ↔ = F ( = m. )

= m. ,эта величина называется импульсом частицы

Импульс системы – это векторная сумма импульсов всех отдельных частиц системы.

=

10.2 Теорема об изменеии импульса системы.

Импульс системы равны сумме импульсов её отдельных частей независимо от того, взаймодействую они между собой или нет.

= → = → = + F_i

F_ik – силы, действующие на и-ю частицу ( внутрение )

F_i – сила, действующая на и-ю частицу со стороны других тел, не входящихся в эту систему ( внешняя ) тогда : = +

Сумма всех внутрених сил. Но по 3-ем закону Ньютона силы взаймодействия между частицами попарно одинаковы по модулю и противоположны по направлению . То есть эта сумма равна 0.

= F_внеш → p₂ – p₁ =

То есть ираращение импульса системы равно импульсу результирующих всех внешних сил за соответствующий промежуток времени.