22. Символический метод расчета цепей переменного тока

За основу символического изображения векторов переменного тока, приняты след. простые положения:

Любой вектор (тока) можноразложить на составляющие (I’I”), направленные по 2м осям прямоугольной системы координат.

+j

I”

I’ +1

-j

Ось абсцисс при символическом изображении векторов будем наз. действительной.

Ось ординат – осью мнимых велечин. Причем составляющие векторов по мнимой оси будем выделять посредством особого множителя символом j. Таким образом в символической орме вектор тока будет равен I = I’+I”

Если некоторый вектор напряжения, направленный по действительной оси, умножить на j, то вектор jU будет повернут относительно к вектору напряжения на угол 90^о против часовой стрелки т.е. в положительную сторону.

Умножение на j² поворачивает на 180^о, а такой поворот переменен знаку вектора. j²U= -U = >

j = - мнимая единица.

Таким образом, при символическом изображении вектор рассматривается как комплексная величина, а плоскость, на которой вектор изображен через действительную и мнимую составляющие, наз. комплексной плоскостью.

Применяются 3 формулы:

1) Алгебраическая форма записи: I = I’ + jI”

2) Триганаметрическая: I = I cosα + jIsinα и после подстановки Эллера: cosα + jsinα = e^jα

3) Показательная: I = Ie^jα

В большинстве случаев можно пользоваться алгебраической формулой, но при возведении в степень и извлечении корня приминять показательную. Для перехода к ней служат простые соотношения I = α= arctg ( )

Положение вектора тока или напряжения на комплексной плоскости определяется его начальной фазой α, последнее относительно произвольно, т.к. зависит от услов. момента начального расчета. При расчете цепи перемен. тока можно принять равной 0 начальную фазу какого-то одного из напряжений либо токов. Тем самым мы принимаем, что вектор этой величины направлен по действительной оси все остальные векторы, определенные при расчете, окажутся ориентированы по отношению к этому вектору.

I=U/r

U_L=IjwL=IjX_L

U_C=I(-j/w_c)=I(-jX_C)

23. Резонанс напряжения

Резонанс напряжений

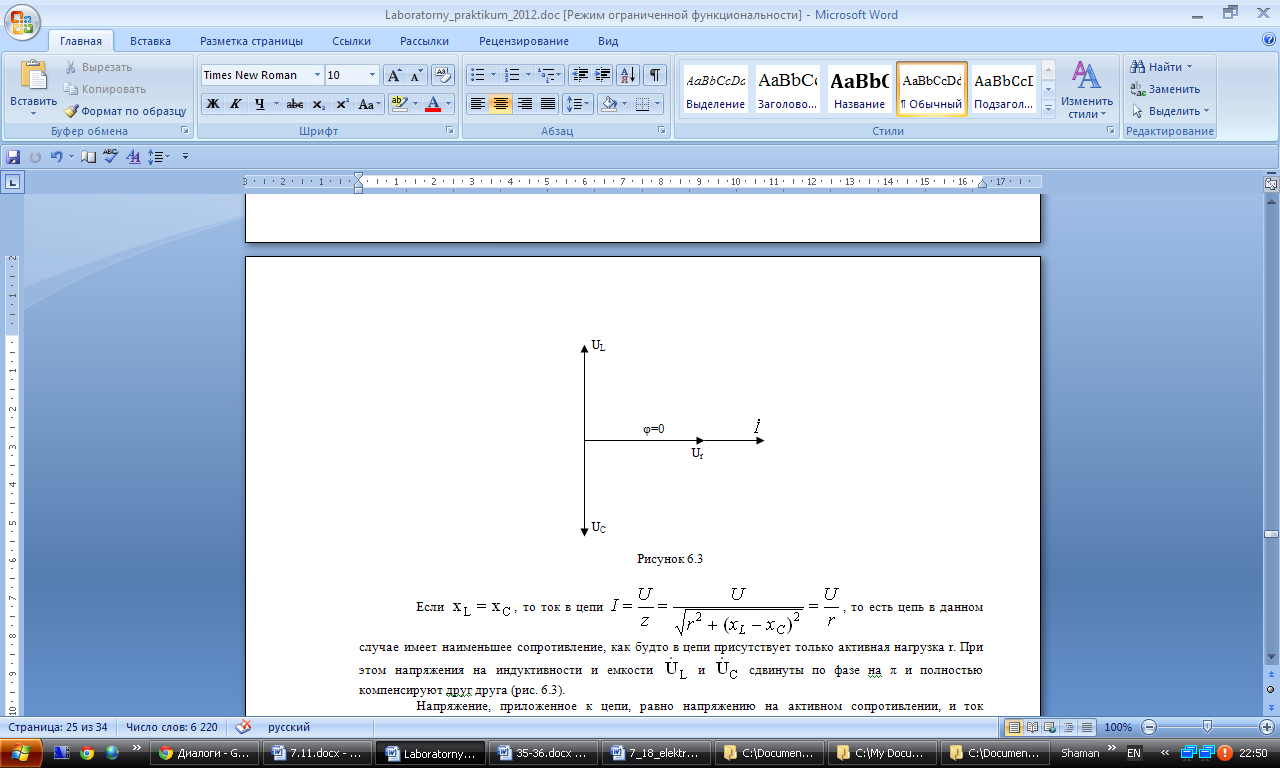
Если , то ток в цепи, то есть цепь в данном случае имеет наименьшее сопротивление, как будто в цепи присутствует только активная нагрузка r. При этом напряжения на индуктивности и емкости и сдвинуты по фазе на π и полностью компенсируют друг друга

Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением. При этом напряжение на индуктивности и емкости может значительно превышать входное напряжение , поэтому резонанс получил название резонанса напряжений.

Отношение выражает добротность контура. Добротность контура показывает, во сколько раз напряжение на индуктивном элементе превышает напряжение на входе схемы двухполюсника. В радиотехнике Q может доходить до 300 и более. Чем больше добротность, тем более острую форму имеют кривые тока и напряжений.

Рисунок 6.4

Из условия следует, что резонанса напряжений можно достичь, изменяя либо частоту приложенного напряжения, либо параметры цепи - индуктивность или емкость. Угловая частота ω_рез, при которой наступает резонанс, называют резонансной угловой частотой: . В лаборатории резонанса напряжений достигают при ω=const, L=const, изменяя емкость С (рис. 6.4). Программа EWB позволяет наблюдать резонанс, меняя любой из перечисленных параметров.

При резонансе напряжений можно отметить следующие моменты:

1. Резонанс напряжений происходит при условии, что входное сопротивление является чисто активным, т.е.: , при . Ток и напряжение совпадают по фазе.

2. Резонанс зависит от L, C и ω. , или .

3. Напряжение источника и падение напряжения на r равны, тогда ,

( ) они находятся в противофазе и взаимно компенсируют друг друга .