8 Метод непосредственного применения законов Кирхгофа

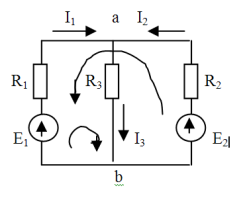
Задаемся условно положительным током в ветвях, затем составляем систему уравнений, равную числу неизвестных токов. По первому закону Кирхгоффа составляем (n-1) число уравнений, где n-число узлов, недостающее число уравнений составляем на основе 2го закона Кирхгоффа

I1 + I2 = I3

E1 = I1R1+ I3R3

E2 – E1 = I2R2 – I1R1

решая полученную систему, получим исходные токи

9. Метод наложения

В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.

При расчете схемы, содержащей несколько ЭДС поочередно полагают равную нулю всей ЭДС кроме одной.

Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.

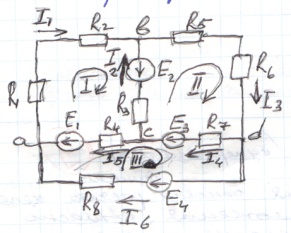
10 Метод контурных токов

При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа, тем самым ,сократив общее число совестно решаемых уравнений. Суть метода рассмотрим на примере:

Разбиваем схему на 3 смешных независимых контуров.Выбираем условно (+) направление обхода в них. В ветвях яв-ся общ для 2-х смежных контуров протекающие токи равны алгебр.сумме 2-х контурных токов. Применим для каждого контура в отдельности 2 закон Кирхгофа и получим систему уравнений равную числу контурных токов.

E₁+E₂=I_к1(R₁+R₂)+(I_к1-I_к2)R₃+(I_к1-I_к3)R₄

E₃-E₂=(I_к2-I₁)R₃+I_к2(R₅+R₆)+(I_к2-I_к3)R₇

E₄-E₁-E₃=I_к3R₈+(I_к3-I_к1)R₄+(I_к3-I_к2)R₇

Входящие в эти уравнения контурные токи удовлетворяют 1З.К. во всех точка разветвления. Полученные ур-я можно представить в виде более удобном для совместного решения:

E₁+E₂=I_к1(R₁+R₂+R₃+R₄)-I_к2R₃-I_к3R₄

E₃-E₂=-I_к1R₃+I_к2(R₃+R₅+R₆+R₇)-I_к3R₇

E₄-E₁-E₃=-I_к1R₄-I_к2R₇+I_к3(R₄+R₇+R₈)

Решая полученную систему рекомендуется метод Крамера. Найдем контурные токи по которым определим токи в ветвях

I₁=I_k1

I₂=I_k2-I_k1

I₃=I_k2

I₄=I_k2-I_k3; I₅=I_k1-I_k3 I₆=I_k3

11. Метод 2х узлов (узлового напряжения)

Этотметод целесообразно принимать в тех случаях, когда схема имеет несколько параллельных ветвей, сходящихся в 2х узловых точках, а также к электрическим цепям, которые в рез-те не сложных преобразований можно привести к схеме с 2 узлами.

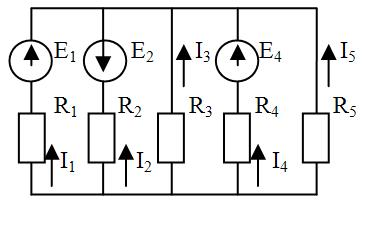
Примем направление токов во всех ветвях одинаковыми (от В к А). Напряжение между 2 узловыми точками назовем узловым напряжением U_ab.

Применим ко всем ветвям 2 закон Кирхгофа:

E₁ - U_ab = I₁R₁ I₁ = (E₁ - U_ab) / R₁ = (E₁ - U_ab)g₁ (1)

-E₂ - U_ab = I₂R₂ I₂ = (-E₂ - U_ab) / R₂ = (-E₂ - U_ab)g₂ (2)

0 - U_ab = I₃R₃ I₃ = ( - U_ab) / R₃ = ( - U_ab)g₃ (3) g = 1/R

E₄ - U_ab = I₄R₄ I₄ = (E₄ - U_ab) / R₄ = (E₄ - U_ab)g₄ (4)

0 - U_ab = I₅R₅ I₅ = ( - U_ab) / R₅ = ( - U_ab)g₅ (5)

Запишем уравнение для данной цепи на основании 1-го закона Кирхгофа.

I₁ + I₂ + I₃ + I₄ + I₅ = 0

(E₁ - U_ab)g₁ + (-E₂ - U_ab)g₂ + ( - U_ab)g₃ + (E₄ - U_ab)g₄ + ( - U_ab)g₅ = 0

E₁g₁ – E₂g₂ + E₄g₄ = U_abg₁ + U_abg₂ + U_abg₃ + U_abg₄ + U_abg₅

U­_ab = ( E₁g₁ – E₂g₂ + E₄g₄ ) / ( g₁ + g₂ + g₃ + g₄ + g₅ ) = ∑E_kg_k / ∑g_k

Произведение E_kg_k для k – ветвей будет брать со знаком минус, если направление ЭДС противоположно по направлению принятому направлению тока.

Определив узловое напряжение U_ab, находим значения токов в отдельных ветвях схемы, используя выражения (1)-(5).

12 Основные определения синусоидального тока (период, цикл, частота) Энергетика основана на передаче энергии на дальние расстояния при помощи электр.поля. Обязательным условием для этого яв-ся возможность простого и с малым потерями преобразования тока большой силы и низкого напряжения в ток малой силы и высокого напряжения(или наоборот). Такое преобразование осуществимо с помощью трансформатора.

Из-за больших преимуществ трансформирования электроэнергетика построена на применении переменного тока. Переменным током можно было бы назвать всякий ток изменяющийся во времени. Но в технике переменный ток принято называть ток, периодически изменяющийся ро величине и направлению. Причем среднее значение этого тока за период равна 0.

Периодическим переменный ток яв-ся потому что спустя промежуток времени называемый периодом Т.

Полный круг изменений переменного тока называется циклом. Следовательно, период это длительность одного цикла переменного тока. Число периодов (циклов) в секунду называется частотой. Это величина обратная периоду. f=1/T {Гц}