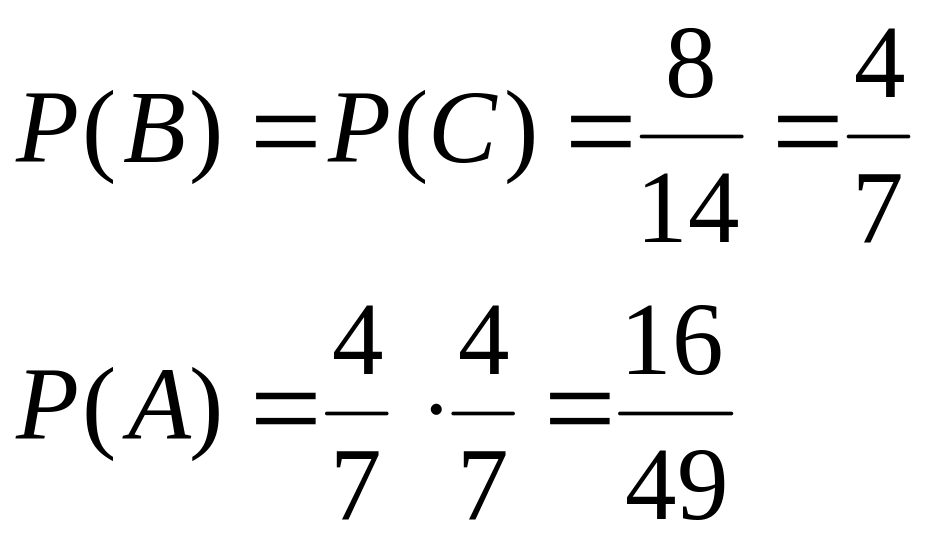III. Основные теоремы теории вероятностей.

Данная тема содержит ряд теорем и формул, использование которых требует четкого понимания их логического содержания и условий применения. Для успешного освоения материалов данной темы необходимо уяснить понятие суммы событий, произведение событий, совместимости и несовместимости событий, зависимости и независимости событий, условной вероятности.

Особое внимание следует уделить полной группе событий и формуле полной вероятности.

При решении задач с использованием теорем сложения и умножения вероятностей необходимо ввести обозначения для событий и составить соотношения между ними, позволяющие определить искомую вероятность. Нужно внимательно следить за выполнением условий применимости той или иной теоремы.

§ 1. Теорема сложения вероятностей несовместимых событий.

Вероятность суммы нескольких несовместных событий равна сумме вероятностей этих событий:

Р(А+В+С) = Р(А) + Р(В) + Р(С)

СЛЕДСТВИЯ:

1.Сумма вероятностей несовместных событий А₁,...,А_n, образующих полную группу, равна единице.

Р(А₁) + Р(А₂)+... +Р (А_n) = 1

2 Сумма вероятностей противоположных событий равна единице Р(А) + Р( ) = 1

Если обозначить Р(А)=Р , Р( ) = q , то Р+q=1.

Эту формулу следует запомнить , так как она многократно будет использоваться в дальнейшем. Рассмотрим следующие задачи:

Задача 1. В ящике 8 белых и 12 красных шаров. Наудачу вынимают три шара. Какова вероятность , что хотя бы один из них белый (событие А).

Решение: А- событие, что хотя бы один из трех шаров- белый. Это событие можно записать так А=В+С+Д, где В- событие, заключающееся в том, что из трех вынутых шаров 1 белый, С- два белых, Д- все три шара белые. События В,С,Д - несовместные.

Р(А)=Р(В+С+Д) = Р(В) + Р(С) + Р(Д)

Задача 2. На оптовую базу поступили однотипные товары с двух предприятий - 3000 штук с первого, 2000 штук - со второго. Согласна оценкам брак на первом предприятии составляет 0,2 %,на втором-0,3 %.Найти вероятность того, что наудачу взяты изделие из не рассортированной продукции окажется бракованным.

Решение: Обозначим через А - событие, заключающееся в том, что взятое бракованное изделие изготовлено первым предприятием, через В- событие, заключающееся в том, что взятое бракованное изделие изготовлено вторым предприятием. С- событие, что наудачу взятое изделие окажется бракованным равно С=А+В, где А и В несовместные события.

Р(С) = Р(А) + Р(В) = 0,002 + 0,003 = 0,005

§ 2.Теорема умножения независимых событий.

Два события называются независимыми, если вероятность появления одного из них не зависит от того, появилось или не появилось другое событие. Несколько событий называются взаимно независимыми (или независимыми в совокупности), если каждое из них и любая комбинация, составленная из остальных (части или всех) событий, являются независимыми событиями.

Если события А₁ ,А ₂,...,А_n взаимно независимы, то и противоположные их события также взаимно независимы.

Вероятность произведения нескольких взаимно независимых событий равна произведению вероятностей этих событий.

Р(А₁А₂,...А_n) = Р(А₁ ) Р(А₂) ... Р(А_n)

Для двух событий Р(АВ) =Р(А)  Р(В)

Задача 1.Два товароведа работают независимо друг от друга. Вероятность пропустить бракованное изделие первым товароведом -0,1; вторым-0,2. Какова вероятность то­го, что при просмотре изделия:

а) оба товароведа не пропустят брак;

б) пропустят бракованное изделие;

Решение: А- событие , что брак пропустил I товаровед, В-II товаровед.

А -событие, что брак не пропустит I товаровед,

В-II товаровед. Так как оба работают независимо друг от друга, то А и В независимые события

А и В также независимы

Задача 2.Бросили монету и игральную кость .Какова вероятность того, что на монете выпал герб, а на кости ­число очков, кратное трем ?

Решение: Обозначим через А событие, что на монете выпал герб, В событие, что на игральной кости выпало число очков кратное трем.

В производимом опыте эти события независимы. Соглас­но классическому определению вероятностей найдем веро­ятности событий А и В.

Нас интересует событие С, заключающееся в одновременном появлении события А и В, то С= АВ. Поэтому Р(С)=Р(АВ)= Р(А) Р(В) =

Задача 3.В урне находятся 8 белых и 6 черных шаров. Из нее извлекаются последовательно два шара , причем после первого извлечения шар возвращается снова в урну. Найти вероятность, что оба вынутых шара - белые.

Решение: Обозначим через А- событие, заключающееся в

том, что появилось два белых шара. Событие В- появление белого шара при первом извлечении. Событие С- появление белого шара при втором извлечении. Тогда А= ВС. Так как после первого извлечения шар возвращается в урну, то события В и С независимы. Поэтому Р(А)=Р(ВС)=Р(В) Р(С).