Ответ: 1/120

13.На каждый из шести одинаковых карточек напечатана одна из следующих букв: а,m,м,р,с,о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных в "одну линию" карточках можно будет прочесть слово "СОРТ" (АТОМ,РОСТ,ТРОС,МАРТ,МОРС,РОТА)

Ответ: 1/360

14.Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость:

­а)оказалась дублем;

б)не есть дубль.

Ответ: (2/9;4/9)

15.Восемь различных групп, расставляются наудачу на одной полке. Найти вероятность того, что две определен­ные книги окажутся поставленными рядом.

Ответ:

16.Библиотечка состоит из десяти различных книг, при­чем пять книг стоят по 40 тенге каждая, три книги- по десять тенге и две книги - по 30 тенге. Найти вероят­ность того, что взятые наудачу две книги стоят 50 тенге.

Ответ:

17.Задумано двузначное число. Найти вероятность того, что задуманным числом окажется:

а)случайно названное двузначное число; Ответ: 1/90

б)случайно названное двузначное число, цифры которого различны; Ответ: 1/81

18.Брошены две игральные кости. Найти вероятности следующих событий:

а)сумма выпавших очков равна семи ;

б)сумма выпавших очков равна восьми, а разность- че­тырем.

в)сумма выпавших очков равна восьми, если извест­но, что их разность равна четырем.

г)сумма выпавших очков равна пяти, а произведе­ние- четырем.

Ответ: 1/6; 1/8; 0,5 ; 1/18.

19.Монета брошена два раза. Найти вероятность то­го, что хотя бы один раз появится "герб".

Ответ: (0,75)

20.В ящике имеется 15 деталей, среди которых 10 ок­рашенных. Сборщик наудачу извлекает три детали. Найти ве­роятность того, что извлеченные детали окажутся окрашен­ными.

Ответ: 24/91.

21.В ящике 100 деталей, из них 10 бракованных. Науда­чу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей:

а)нет бракованных;

б)нет годных;

Ответ: а) 0,65 б)0,00005

22.Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

Ответ: (0,3)

23.На складе имеется 15 кинескопов ,причем 10 из них изготовлены Львовским заводом. Найти вероятность то­го, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.

Ответ: 0,4

24.В группе 12 студентов, среди которых 8 отлични­ков. По списку наудачу отобраны 9 студентов. Найти веро­ятность того, что среди отобранных студентов пять от­личников.

Ответ:14/55

25.В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти веро­ятность того, что среди двух извлеченных изделий окажут­ся:

а)одно окрашенное изделие;

б)два окрашенных изделия;

в)хотя бы одно окрашенное изделие;

Ответ: (0,6;0,3;0,9)

26.В "секретном" замке на общей оси четыре дис­ка, каждый из которых разделен на пять секторов, на ко­торых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.

Ответ: 1/5⁴.

27.На 8 одинаковых карточках написаны соответствен­но числа 2,4,6,7,8,11,12,13.Наугад берутся две карточ­ки. Определить вероятность того, что образованная из 2-х полученных чисел дробь, сократима.

Ответ:

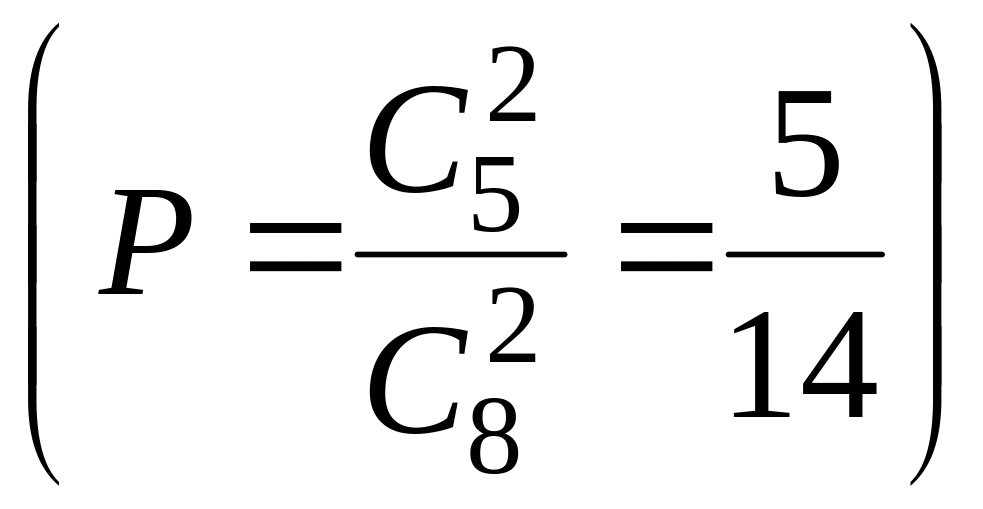
28.В шкафу находятся 10 пар ботинок различных сор­тов. Из них случайно выбираются 4 ботинка. Найти вероят­ность того, что среди выбранных ботинок отсутствуют пар­ные.

Ответ: = 0,6935

29.Профессор вызвал через старосту на обязательную консультацию 3-х студентов из 6 отстающих. Староста забыл фамилии вызванных студентов и послал на удачу 3-х отс­тающих студентов. Какова вероятность того, что староста послал именно тех студентов ,которых вызвал профессор?

Ответ:1/120

30.В магазине работает 10 продавцов, из них 6 жен­щин. В смену заняты 3 продавца. Найти вероятность то­го, что в наудачу выбранную смену войдут все 3 продавца мужчины.

Ответ: 1/30

31.В группе 25 студентов. Вызываются во время заня­тий 3 студента. Полагая, что вызов производится случай­но, определить какова вероятность того, что будут вызва­ны данные 3 студента в определенном порядке.

Ответ: 1/13 800

32.Буквы А,А,А,А, Р,К,Н,Г,Д написаны на отдельных карточках. Какова вероятность того, что при случайном расположении букв в ряд, мы получаем слово "КАРАГАНДА".?

Ответ: 1/15 120

33.В коробке 6 белых и 4 красных карандаша. Наудачу извлекают 5 карандашей. Какова вероятность того, что 2 из них белые, а 3 красные.

Ответ: 5/21

34.На карточках написаны буквы И,К,М,Н,О,О,С,Т,Э. Эти карточки выкладывают наудачу подряд. Какова вероятность того, что при этом получится слово "ЭКОНОМИСТ"?