V.Элементы теории корреляции.

Установление количественных зависимостей (связей) между изучаемыми признаками имеет очень важное значение для различных экономических исследований. Связь между признаками может быть функциональной (полной) и корреляционной (статистической).

Функциональной называется такая связь между признаками, при которой каждому значению одной (аргумента) соответствует строго определенное значение другой переменной (функции). В социально-экономических явлениях функциональные связи между признаками встречаются весьма редко. Здесь обычно встречаются такие связи между признаками, при которых значению одного из них соответствует несколько значений другого. Такая связь называется корреляционной. Корреляционная связь проявляется при большом числе наблюдений, выражается соответствующими математическими уравнениями. Различают прямолинейную и криволинейную, прямую и обратную, простую и множественную корреляционные связи. С помощью метода корреляционного анализа решаются две основные задачи:

1. определение формы и параметров уравнения связи

2. измерение тесноты связи

Выбор уравнения для изучения связей между признаками является наиболее сложным и ответственным моментом корреляционном анализе. При парной корреляции математическое уравнение связи может быть установлено с помощью построения графиков, составления корреляционных таблиц, пересмотра различных функций.

В экономических исследованиях часто рассматривается прямолинейная зависимость, выражаемая уравнением прямой линии - выровненные значения результативного признака (зависимая перемен.),х- значение факторного признака (независимая перемен.), b-коэффициент регрессии, показывающий среднее изменение зависимой переменной при изменении независимой переменной на единицу. Если b>0, то связь прямая, если b<0, то связь обратная. Это уравнение называется уравнением регрессии или корреляционным уравнением. Параметры уравнения а и b находят методом наименьших квадратов, дающим возможность найти такую теоретическую линию регрессии, которая проходит наиболее близко к точкам корреляционного поля, изображающим фактические данные, т.е. дает наименьшую сумму квадратов отклонений фактических значений результативного признака от выровненных значений: .

Для определения коэффициентов а и b необходимо решить систему нормальных уравнений:

Можно коэффициенты а и b найти по формулам:

где

.

Для криволинейной зависимости также решается система нормальных уравнений. Например, для параболы эта система имеет вид:

для гиперболы

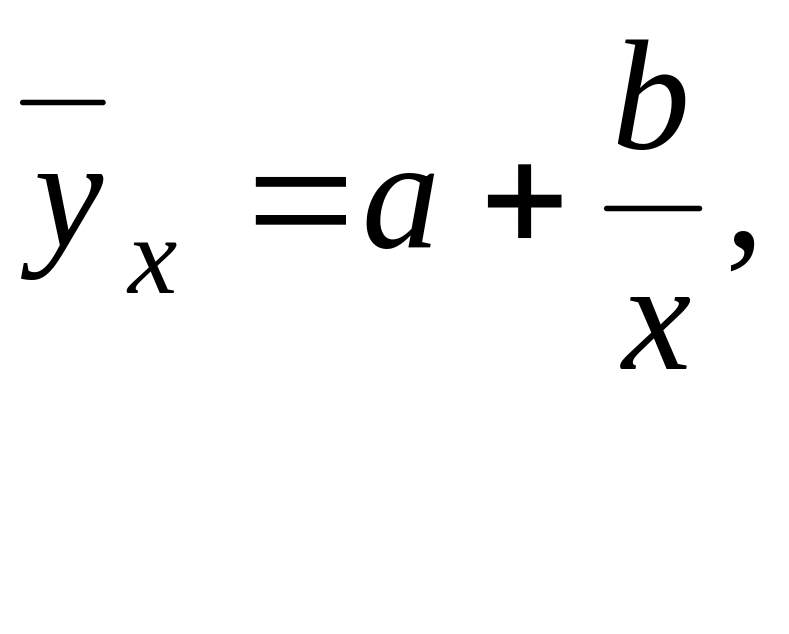
Уравнения корреляционной связи используют для расчета теоретической линии регрессии и ожидаемых значений зависимой непременной при соответствующих значениях фактора.

Для определения степени тесноты связи между признаками используется коэффициент корреляции.

При парной линейной зависимости коэффициент корреляции r определяется по формуле: , где .

Коэффициент корреляции, применяемый для оценки тесноты при любой форме связи можно вычислить по формуле ;

Если каждому значению отвечает несколько значений х, а каждому - несколько значений у, то эти данные упорядочивают и записывают в виде корреляционной таблицы:

y x	у1	у2	…	уn
x1	n11	n12	…	n1n
x2	n21	n22	…	n2n
…	…	…	…	…	…
xm			…

Здесь - частоты, показывающие, сколько раз повторяются парные значения Среднее арифметическое значение величины У, вычисленное при условии, что Х принимает фиксированное значение, называется условным средним и обозначается Аналогично определяется условное среднее . В этом случае можно записать уравнение линии регрессии У на Х или Х на У. Если обе линии регрессии-прямые, то корреляцию называют линейной. Выборочное (теоретическое) уравнение прямой линии регрессии У на Х имеет вид: , а уравнение линии регрессии Х на У: .

Если данные наблюдений над признаками Х и У заданы в виде корреляционной таблицы с равностоящими вариантами, то для упрощения всех расчетов целесообразно перейти к условным вариантам:

где С₁ и С₂ – ложные нули, h₁ и h₂ - шаги вариант Х и У соответственно. В том случае выборочный коэффициент корреляции вычисляют по формуле:

Величины можно найти либо методом произведений, рассмотренным ранее (при большом числе данных), либо непосредственно по формулам:

Затем определяются величины

Пример 9. Найти выборочное уравнение прямой линии регрессии У на Х по данным, приведенным в корреляционной таблице:

х	10	14	18	22	26	30	ny
у
10	5	1	2				6
15		6	5				8
20			2	40	5		50
25				8	7		17
30				4	7	8	19
nx	5	7	9	52	19	8	100

Решение: составим таблицу в условных вариантах, взяв С₁=22, С₂=20,

h₁=14-10=4, h₂=15-10=5.

u v	-3	-2	-1	0	1	2		n
-2	5	1	2					6
-1		6	5					8
0			2	40	5			50
1				8	7			17
2				4	7	8		19
nu	5	7	9	52	19	8	100

По этой таблице вычислим величины:

Для вычисления коэффициента корреляции составим расчетную таблицу:

В правых верхних углах клеток таблицы записаны произведения , а в левых нижних углах произведения Затем складывают все числа в правых верхних углах каждой строки и записывают в столбце U . Аналогично находят суммы чисел в левых нижних углах по каждому столбцу и записывают их в строке V.

u	-3	-2	-1	0	1	2	u	u

-2							-17	34
-1							-14	14
0							0	0
1							5	5
2							23	46
V	-10	-8	0	16	21	16		=u =99
uV	30	16	0	0	21	32	= uV=99	контроль

Вычисляет коэффициент корреляции:

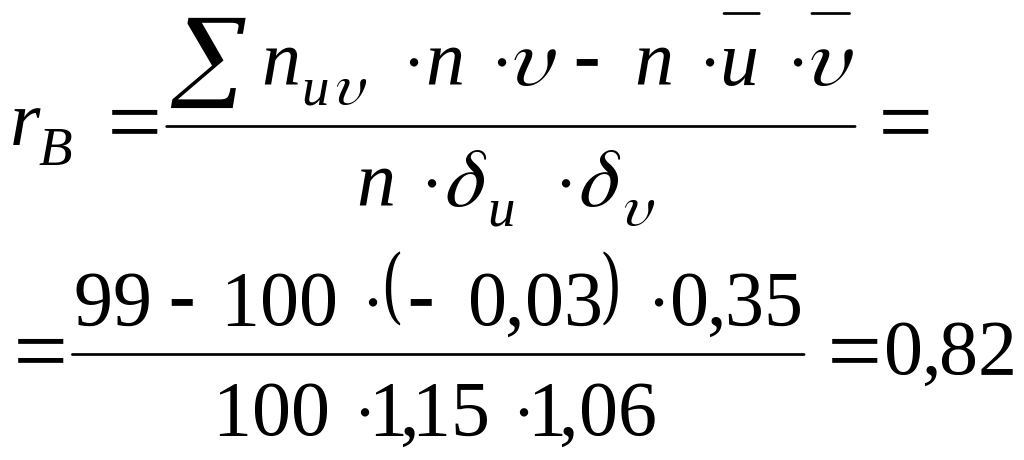
Далее находим:

Подставим найденные значения в уравнение регрессии, получим:

или окончательно получим уравнение: