IV. Статистическая проверка статистических гипотез.

Статистической называется гипотеза о виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) называется выдвинутая гипотеза Н₀.

Конкурирующей (альтернативной) называется гипотеза Н₁, которая противоречит нулевой.

В результате проверки гипотез могут быть допущены ошибки двух рядов:

Ошибка I ряда состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки I называется уровнем значимости и обозначается .

Ошибка II ряда состоит в том, что будет принята неправильная гипотеза. Вероятность ошибки II ряда обозначается .

Статистическим критерием называется случайная величина K, которая случай для проверки гипотезы.

Наблюдаемым (эмпирическим ) значением K_набл. называется значение критерия, вычисленное по выборкам.

Критической областью называется совокупность значений критерия, при которых отвергается нулевая гипотеза.

Областью принятия гипотезы (о.д.з) называется совокупность значений критерия, при которых принимают нулевую гипотезу.

Основной принцип проверки статистических гипотез:

если К_набл.  критической области, то Н₀ отвергают ,

если К _набл.  области принятия гипотезы, то гипотезу принимают.

Критическими точками (границами) К_кр. называются точки, отделяющие критическую область от области принятия гипотезы.

Правосторонней называется критическая область, определяемая неравенством , а левосторонней, если К_кр, где _кр0.

Левосторонняя или правосторонняя критическая область называется односторонней.

Двусторонней называется критическая область определяемая неравенствами Кк₁, к₂, где к₂  к₁.

Для отыскания критической области задают уровень значимости  и находят критические точки, исходя из соотношений:

1. для правосторонней кр. обл. :

2. для правосторонней :

3. для двусторонней симметричной области:

; ,

Для проверки статистических гипотез применяют критерии согласия, т.е. правила, позволяющие принять или отвергнуть выдвинутую гипотезу. Так как нормальное распределение встречается довольно часто, то наиболее часто проверяют гипотезу о соответствии выборочного распределения нормальному. Из множества критериев согласия о распределениях наиболее мощным является критерий ² Пирсона (критерий «хu-квадрат» Пирсона).

Пусть в результате n наблюдений получено статистическое распределение выборки:

Хi	Х1	Х2	…	XS
ni	n1	n2	…	nS

Выдвинем статистическую гипотезу: «Генеральная совокупность , из которой извлечена выборка, имеет нормальное распределение».

Критерий Пирсона представляет собой следующее правило:

Для того, чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:

1. вычислить выборочную среднюю и выборочное среднее квадратическое отклонение ;

2. вычислить теоретические частоты формуле: ,

где n-объем выборки,

h- шаг (разность между двумя соседними равноотстоящими вариантами),

(находят по таблице- приложение 1)

3. вычислить наблюдаемое значение критерия

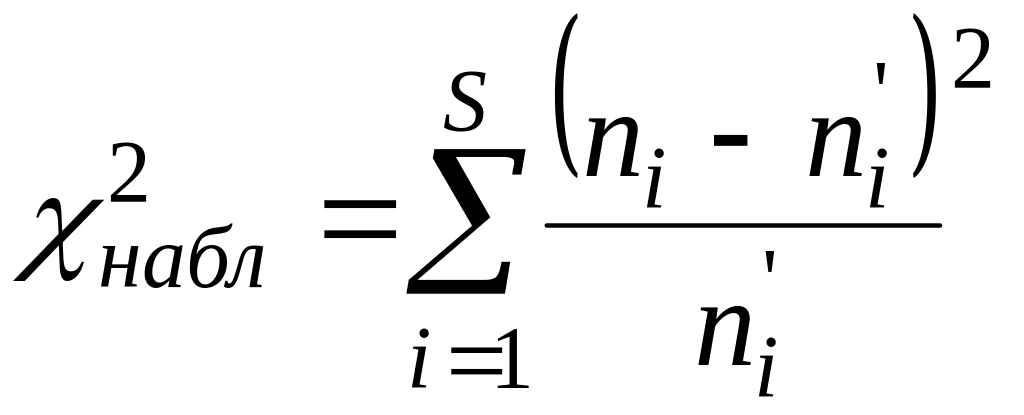
4. вычислить число степеней свободы где S- число групп, на которые разбита выборка;

5. выбрать уровень значимости ;

6. по таблице критических точек распределения найти критическую точку

7. Если , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо (случайно).

8. Если то гипотезу о нормальном распределении генеральной совокупности отвергают, т.е. эмпирические и теоретические частоты различаются значимо.

Пример 8. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки:

Хi	-35	-25	-15	-5	5	15	25	35	45	55
ni	4	5	11	24	39	31	28	9	5	4

1. Для вычисления и воспользуемся методом произведений.

Составим расчетную таблицу:

Хi	ni	ti	ni  ti	ni  ti2
-35	4	-4	-16	64
-25	5	-3	-15	45
-15	11	-2	-22	44
-5	24	-1	-24	24
+5	39	0	0	0
+15	31	1	31	31
25	28	2	56	112
35	9	3	27	81
45	5	4	20	80
55	4	5	20	100
	n=160		77	581

где С=5 (варианта с наибольшей частотой 39), h=15-5=10.

2. Вычислим теоретические частоты.

Составим расчетную таблицу:

i	Xi	Xi-
1	-35	-44,8	-2,43	0,0208	2
2	-25	-34,8	-1,89	0,0669	6
3	-15	-24,8	-1,35	0,1604	14
4	-5	-14,8	-0,8	0,2897	25
5	5	-4,8	-0,26	0,3857	34
6	15	5,2	0,28	0,3836	33
7	25	15,2	0,83	0,2827	25
8	35	25,2	1,37	0,1561	14
9	45	35,2	1,91	0,0644	6
10	55	45,2	2,46	0,0194	2

2. Составим расчетную таблицу для вычисления наблюдаемого значения критерия

1	4	2	2	4	2
2	5	6	-1	1	0,167
3	11	14	-3	9	0,643
4	24	25	-1	1	0,04
5	39	34	5	25	0,735
6	31	33	-2	4	0,121
7	28	25	3	9	0,36
8	9	14	-5	25	1,786
9	5	6	-1	1	0,167
10	4	2	2	4	2
	160

2. Вычислим число степеней свободы .

3. По таблице (приложение 5) находим

Так как то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо.

Этот вывод можно наглядно продемонстрировать графически. Построим полигон частот, т.е. ломаную линию, соединяющую точки с координатами , а затем на этом же графике построим теоретическую (нормальную) кривую, для чего плавной линией соединим точки с координатами .