Неравенство Чебышева.

Для любой случайной величины Х, имеющей конечную дисперсию, при любом >1 имеют место

неравенства:

Приведенные неравенства дают не точное значение соответствующей вероятности, а только ее оценку сверху или снизу.

Теорема Чебышева.

Если х₁,х₂,…,х_n- попарно независимые случайные величины, имеющие конечное математическое ожидание и равномерно ограниченные дисперсия (дисперсии не превышают постоянной С), до для любого >0 имеем

то есть при неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины: имеющий ограниченную дисперсию, сходится по вероятности к ее математическому ожиданию.

Теорема Бернулли.

Пусть производится n независимых испытаний , m- число наступления события А в этих испытаниях, р-вероятность наступления события А в каждом испытании. Тогда для любого >0 имеем:

т.е. относительная частота случайного события сходится по вероятности к вероятности этого события в единичном испытании.

ЗБЧ является связующим звеном между теорией вероятностей как математической наукой и закономерностям случайных явлений при массовых наблюдениях за ними. Он играет очень важную роль в практических применениях теории вероятностей к явлениям природы и техническим процессам, связанным с массовым производством. В практических исследованиях очень важно знать в каких случаях можно гарантировать, что вероятность события окажется или достаточно малой или очень близкой к 1.

Рассмотрим последовательность случайных величин, распределенных по биномиальному закону:

Пусть х=х₁+х₂₊…+х_n.

Имеет место теорема:

Для биномиального распределения вероятностей существует предельное (при ) распределение и это распределение является нормальным.

где

В частности:

где Ф(t)- функция Лапласа.

Решение задач:

Задача 1. Пусть х₁,х₂,…,х_n- -последовательность независимых случайных величин, причем х_n принимает значения и с вероятностями ;

соответственно. Применим ли к этой последовательности ЗБЧ?

Решение: Для этого, чтобы к последовательности случайных величин была применима теорема Чебышева, должны быть выполнены следующие условия:

1. случайные величины попарно независимы;

2. математические ожидания конечные;

3. дисперсии равномерно ограниченные.

Первое условия выполнено по условию задачи.

Проверим условие 2.

Значит условие 2 выполнено.

Найдем дисперсии.

Для этого составим закон распределения величин

		0
р

Тогда

Условие 3 также выполнено, значит, к данной последовательности случайных величин применим ЗБЧ.

Задача 2. Средняя урожайность пшеницы составляет 40 ц. с гектара. Какую урожайность можно ожидать с вероятностью, не меньшей, чем 0,5?

Решение: Пусть Х- урожайность пшеницы, тогда М(Х)- средняя урожайность. Применим неравенство Чебышева (1^')

. По условию задачи М(Х)=40, тогда .

Найдем искомое .

Значит, т.е. следует ожидать урожайность ц. с гектара.

Задача 3.Вероятность изготовления бракованной детали равна 0,1. Какое наименьшее количество деталей нужно взять, чтобы с вероятностью, большей 0,9, можно было утверждать , что доля бракованных деталей будет отличаться от вероятности изготовления бракованной детали не более, чем на 0,01?

Решение: Изготовление бракованной детали можно рассматривать как случайную величину, имеющую два возможных значения 0 и 1, которым соответствуют вероятности q=0,9 и р=0,1. Тогда вся совокупность из n деталей описывается последовательностью одинаково распределенных случайных величин.

Используем неравенство Чебышева (2^')

или

Ответ: наименьшее число деталей 9000.

Задача 4. Для определения среднего веса зерна взяли 1000 зерен. Установлено, что среднее квадратическое отклонение веса зерна на превышает 0,04 г. оценить вероятность того, что средний вес отобранных зерен будет отличаться от математического ожидания этого среднего не более чем на 0,002 г .?

Решение. Обозначим , где

- случайные величины.

По условию задачи дано, что

Тогда

Используем неравенство Чебышева

Задачи

1. В коробке имеются 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. а)Найдите закон распределения случайной величины х, равной числу красных карандашей в выборке. б)Постройте многоугольник распределения. в)Найдите вероятность события

2. Из 25 контрольных, среди которых 5 оценены на «отлично», наугад извлекают 3 работы. Найдите закон распределения дискретной случайной величины х, равной числу оцененных на «отлично» работ среди извлеченных. Чему равна вероятность события х>0?

3. Имеются 5 ключей, из которых только один подходит к замку. Найдите закон распределения случайной величины х, равной числу проб при открывании замка, если испробованный ключ в последующих опробованных не участвует.

4. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 2 детали. Найдите закон распределения случайной величины, равной числу стандартных деталей в выборке.

5. Автоматическая телефонная станция обслуживает 1000 телефонных точек. Вероятность того, что в течение 5 мин на АТС поступит вызов из телефонной точки, равна 0,005. Найдите закон распределения случайной величины х, равной числу вызовов, поступивших на АТС в течение 5 мин. Чему равна вероятность того, что в течение 5 мин. а)на АТС поступит хотя бы один вызов; б) более 4 вызов?

6. Даны два закона распределения независимых случайных величин:

х	2	3	5
р	0,1	0,3	0,5

х	1	2
р	0,3	0,7

Проверить равенство Д(2Х-3У)=4Д(Х)+9Д(У).

7. Даны законы распределения двух независимых случайных величин:

х	2	3
р	0,1	0,9

х	1	2	-1
р	0,1	0,3	0,6

Найти М(2Х-У) и Д(3У+Х).

8. Задан закон распределения случайной величины Х:

х	2	3	5	6	7	10
р	0,4	0,2	0,2	0,05	0,1	0,05

Найти М(Х), Д(Х),М(2Х²+3).

9. Задан закон распределения случайной величины Х:

х	1	2	3
р	0,3	0,5	0,2

Проверить неравенство: Д(Х²-Х)=Д(Х²)+Д(Х).

10. Задан закон распределения случайной величины Х:

х	1	2	3
р	0,2	0,3	0,5

Проверить неравенство: Д(2Х+5)=4Д(Х).

11.Даны законы распределения независимых

случайных величин:

х	0	1	2	3
р	0,1	0,6	0,2	0,1

у	0	1	2
р	0,5	0,3	0,2

Проверить выполнение равенства:

Д(Х-У)=Д(Х)+Д(У)

12.Дискретная случайная величина задана законом распределения:

х	-1	0	1	2
р	0,2	0,1	0,3	0,4

Найти М(У) и Д(У) случайной величины У=2^х

13.Задан закон распределения случайной величины:

х	-2	0	1	2
р	0,1	0,5	0,3	0,1

Найти М(Х),Д(Х) и М(Х²-3Х).

14.Задан закон распределения случайной величины Х:

х	2	3	5	6
р	0,4	0,3	0,2	0,1

Найти и Д(3Х-5)

15.Задан закон распределения случайной величины Х:

х	2	4	5	6	8	20
р	0,4	0,25	0,2	0,05	0,05	0,05

Найти и М(4Х²-1).

№№ 16-23.Случайная величина Х задана интегральной функцией распределения F(x).Требуется найти:

1. плотность вероятности f(x);

2. математическое ожидание и дисперсию;

3. вероятность того, что Х примет значение, принадлежащее интервалу (а;b).

4. построить графики функций F(x) и f(x).

16. 17.

18. 19.

20. 21.

22. 23.

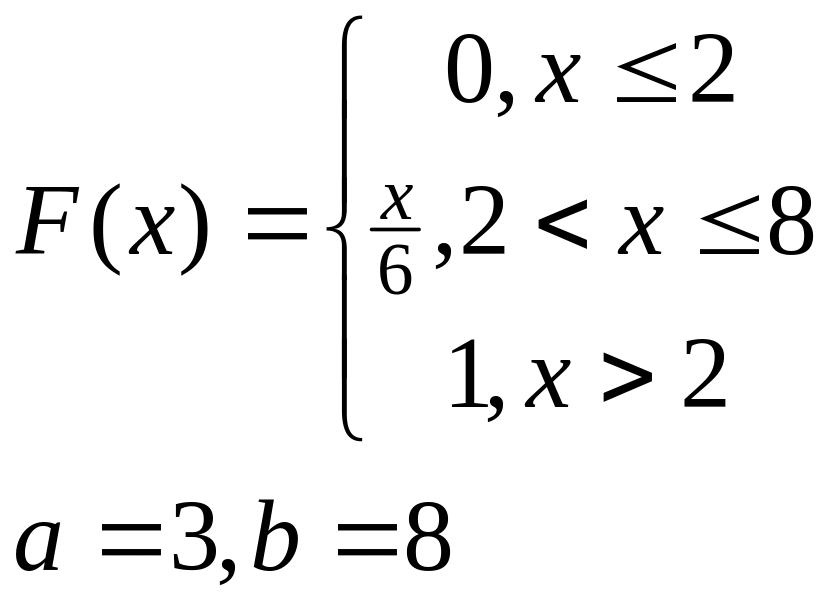
24.Кривая распределения случайной величины Х задана следующим рисунком. Найти:

а)постоянный параметр С;

б)функцию распределения F(x).

в)М(Х).

25.Случайная величина Х задана плотностью вероятности f(x)=c(x²+2x)в интервала (0;1) f(x)=0. Найти:

а) параметр С; б) М(Х).

26. Кривая распределения случайной величины х изображена на рисунке. Найти:

а) параметр С;

б) М(Х) и Д(Х)

27. Найти математическое ожидание и дисперсию случайной величины х, распределенной равномерно в интервале (2;8).

28.Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 7 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 4 мин.

29.Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более, чем на 20 секунд.

30.Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка:

а) меньшая 0,04;

б) большая 0,05

31. Ребро куба х измерено приближенно, причем . Рассматривая ребро куба как случайную величину Х, распределенную равномерно в интервале (а,b), найти математическое ожидание и дисперсию объема куба.

32.Шкала угломерного инструмента имеет цену деления в 1^о.Отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Пусть случайная величина х, допущенная при отсчете, ошибка. Найдите функцию распределения F(x) и плотность вероятности f(x). Найдите вероятность того, что допущенная при отсчете ошибка превзойдет 20^'.

33. Случайная величина х распределена по нормальному закону с параметрами a=0 и . Напишите выражения для плотности вероятности f(x) и функции распределения F(x). Используя таблицу для функции Лапласа, найдите вероятность события 1,25 .

34.Плотность вероятности нормально распределенной случайной величины х имеет вид:

Найдите коэффициент с и параметр ; напишите функцию распределения F(x); найдите вероятность попадания случайной величины х в промежуток [2;5].

35.Случайная величина х распределена по нормальному закону с параметрами а и . В каждом из следующих четырех пунктов а),б),в),г) напишите плотность вероятности и функцию распределения; в одной и той же системе координат постройте кривые распределения; пользуясь «правилом трех сигм», найдите интервал, в который попадает случайная величина х с практической достоверностью (с вероятностью 0,9973).

36.Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение заключенное в интервале (12;14).

37.Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 мм. и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

Указание. Из равенства предварительно найти

38.Случайная величина х может принимать только неотрицательные значения, а ее среднее значение равно 100. С помощью леммы Чебышева оцените снизу вероятность того, что в результате опыта величина х примет значение, меньшее 120.

39.Среднее значение веса изделия данного вида равно 50 г. С помощью леммы Чебышева оцените снизу вероятность того, что наудачу взятое изделие имеет вес меньше 90 г.

40.Средняя температура в квартире в период отопительного сезона равна 20⁰С, а среднее квадратическое отклонение равно 2⁰С. С помощью неравенства Чебышева оцените снизу вероятность того, что температура в квартире отклонится от средней по абсолютной величине менее чем на 4⁰С.

41.Вероятность получения с конвейера изделия высшего качества равна 0,6. Оцените вероятность того, что среди 600 изделий, полученных с конвейера, содержится от 340 до 380 изделий высшего качества. Оценку произведите, используя: а) неравенство Чебышева; б) интегральную приближенную формулу Лапласа.

42.Длина изготавливаемых изделий представляет случайную величину, среднее значение которой равно 90 см. Дисперсия этой величины равна 0,0225. Оцените вероятность того, что: а) отклонение длины изготовленного изделия от ее среднего значения по абсолютной величина не превзойдет 0,4 см; б) длина изделия выразится числом, заключенным между 89,7 и 90,3 см.

43.Дисперсия каждой из 1000 независимых случайных величин равна 4. Оцените вероятность того, что отклонение средней арифметической этих случайных

величин от средней арифметической их математических ожиданий по абсолютной величине окажется меньше чем 0,2.

44.Дискретная случайная величина х- число мальчиков в семьях с 5 детьми. Предполагая равновероятными рождения мальчика и девочки:

а)найдите закон распределения х;

б) постройте многоугольник распределения;

в) найдите вероятности событий:

А- в семье не менее 2,но более 3 мальчиков;

В- не более 3 мальчиков;

С- более одного мальчика.

45.С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успе­вает сделать не более 4 выстрелов. Дискретная случайная величина х- число промахов.

а)Найдите закон распределе­ния х;

б)Постройте многоугольник распределения;

в) Най­дите вероятности событий: х< 2; х3 ; 1< x 3;