11.Оптика.

Оптика – раздел физики, изучающий свойства и физическую природу света, а также его взаимодействие с веществом. Учение о свете принято делить на три части:

• геометрическая или лучевая оптика, в основе которой лежит представление о световых лучах;

• волновая оптика, изучающая явления, в которых проявляются волновые свойства света;

• квантовая оптика, изучающая взаимодействие света с веществом, при котором проявляются корпускулярные свойства света.

11.1.Основные законы геометрической оптики.

Основные законы геометрической оптики были известны задолго до установления физической природы света.

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света.

На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а часть пройдет через границу и продолжит распространяться во второй среде.

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред: 

Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г.

Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: 

n = n2 / n1.

Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ₁к скорости их распространения во второй среде υ₂: 

Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде: 

Рисунок иллюстрирует законы отражения и преломления света.

Законы отражения и преломления: γ = α;n1 sin α = n2 sin β.

Среду с меньшим абсолютным показателем преломления называют оптически менее плотной.

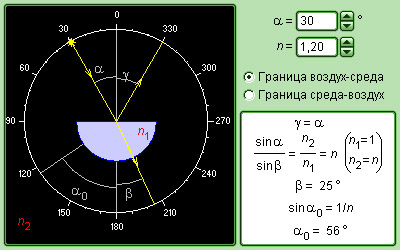
При переходе света из оптически более плотной среды в оптически менее плотную n₂ < n₁ (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол α_пр, который называется предельным углом полного внутреннего отражения (см. рис. 3.1.2).

Для угла падения α = α_пр  sin β = 1; значение sin α_пр = n₂ / n₁ < 1.

Если второй средой является воздух (n₂ ≈ 1), то формулу удобно переписать в виде 

sin αпр = 1 / n,

где n = n₁ > 1 – абсолютный показатель преломления первой среды.

Для границы раздела стекло–воздух (n = 1,5) критический угол равен α_пр = 42°, для границы вода–воздух (n = 1,33) α_пр = 48,7°.

Полное внутреннее отражение света на границе вода–воздух; S – точечный источник света

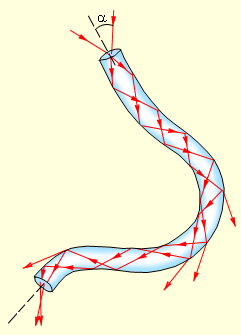
Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рис 3.1.3). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.

Распространение света в волоконном световоде. При сильном изгибе волокна закон полного внутреннего отражения нарушается, и свет частично выходит из волокна через боковую поверхность

Модель. Отражение и преломление света

Скорость света в свободном пространстве (вакууме) с, скорость распространения любых электромагнитных волн (в т. ч. световых); одна из фундаментальных физических постоянных, огромная роль которой в современной физике определяется тем, что она представляет собой предельную скорость распространения любых физических воздействий и инвариантна (т. е. не меняется) при переходе от одной системы отсчёта к другой. Никакие сигналы не могут быть переданы со скоростью, большей с, а со скоростью с их можно передать лишь в вакууме. Величина с связывает массу и полную энергию материального тела; через неё выражаются преобразования координат, скоростей и времени при изменении системы отсчёта (Лоренца преобразования); она входит во многие другие соотношения. Под С. с. в среде с' обычно понимают лишь скорость распространения оптического излучения (света); она зависит от преломления показателя среды n, различного, в свою очередь, для разных частот v излучения (дисперсия света); с'(n) = c/n (n). Эта зависимость приводит к отличию групповой скорости от фазовой скорости света в среде, если речь идёт не о монохроматическом свете (для С. с. в вакууме эти две величины совпадают). Экспериментально определяя с', всегда измеряют групповую С. с. либо т. н. скорость сигнала, или скорость передачи энергии, только в некоторых специальных случаях не равную групповой.

Как можно более точное измерение величины с чрезвычайно важно не только в общетеоретическом плане и для определения значений других физических величин, но и для практических целей (см. ниже). Впервые С. с. определил в 1676 О. К. Рёмер по изменению промежутков времени между затмениями спутника Юпитера Ио. В 1728 то же проделал Дж. Брадлей, исходя из своих наблюдений аберрации света звёзд. На Земле С. с. первым измерил - по времени прохождения светом точно известного расстояния (базы) - в 1849 А. И. Л. Физо. (Показатель преломления воздуха очень мало отличается от 1, и наземные измерения дают величину, весьма близкую к с.) В опыте Физо пучок света периодически прерывался вращающимся зубчатым диском, проходил базу (около 8 км) и, отразившись от зеркала, возвращался на периферию диска. Падая при этом на зубец, свет не достигал наблюдателя, попадая в промежуток между зубцами, - регистрировался наблюдателем. По известным скоростям вращения диска определялось время прохождения светом базы. Физо получил с = 315 300 км/сек.

В 1862 Ж. Б. Л. Фуко реализовал высказанную в 1838 идею Д. Араго, применив вместо зубчатого диска быстровращающееся (512 об/сек) зеркало. Отражаясь от зеркала, пучок света направлялся на базу и по возвращении вновь попадал на это же зеркало, успевшее повернуться на некоторый малый угол. При базе всего в 20 м Фуко нашёл, что С. с. равна 298000 = 500 км/сек. Схемы и основные идеи опытов Физо и Фуко были многократно использованы на более совершенной технической основе др. учёными, измерявшими С. с. Наибольшего развития метод Фуко достиг в работах А. Майкельсона (1879, 1902, 1926). Полученное им в 1926 значение с = 299/96 = 4 км/сек было тогда самым точным и вошло в интернациональные таблицы физических величин.

Измерения С. с. в 19 в. не только выполнили свою непосредственную задачу, но и сыграли чрезвычайно большую роль в физике. Они дополнительно подтвердили волновую теорию света, уже достаточно обоснованную другими экспериментами (Фуко, 1850, сравнение С. с. одной и той же частоты n в воздухе и воде), а также установили тесную связь оптики с теорией электромагнетизма - измеренная С. с. совпала со скоростью электромагнитных волн, вычисленной из отношения электромагнитной и электростатических единиц электрического заряда (опыты В. Вебера и Ф. Кольрауша в 1856 и последующие более точные измерения Дж. К. Максвелла). Последнее явилось одним из отправных пунктов при создании Максвеллом электромагнитной теории света в 1864-73. Кроме того, измерения С. с. вскрыли глубокое противоречие в основных теоретических посылках физики того времени, связанных с представлением о мировом эфире. Эти измерения давали аргументы в пользу взаимоисключающих гипотез о поведении эфира при движении через него материальных тел (анализ явления аберрации света английским физиком Дж. Б. Эри в 1871 и Физо опыт 1851, повторённый в 1886 Майкельсоном и Э. Морли, результаты которых поддерживали концепцию частичного увлечения эфира; Майкельсона опыт 1881 и 1887 - последний совместно с Морли, - отвергший какое-либо увлечение эфира). Разрешить это противоречие удалось лишь в специальной теории относительности (А. Эйнштейн, 1905).

В современных измерениях С. с. используется модернизированный метод Физо (модуляционный метод) с заменой зубчатого колеса на электрооптический, дифракционный, интерференционный или какой-либо иной модулятор света, полностью прерывающий или ослабляющий световой пучок. Приёмником излучения служит фотоэлемент или фотоэлектронный умножитель. Применение лазера в качестве источника света, ультразвукового модулятора со стабилизированной частотой и повышение точности измерения длины базы позволили снизить погрешности измерений и получить значение с = 299792,5 = 0,15 км/сек. Помимо прямых измерений С. с. по времени прохождения известной базы широко применяются т. н. косвенные методы, дающие ещё большую точность. Так, методом микроволнового вакуумированного резонатора (английский физик К. Фрум, 1958) при длине волны излучения l = 4 см получено значение с = 299792,5 =? 0,1 км/сек. Погрешность определения С. с. как частного от деления независимо найденных l и n атомарных или молекулярных спектральных линий ещё меньше. Американский учёный К. Ивенсон и его сотрудники в 1972 по цезиевому стандарту частоты нашли с точностью до 11 знаков частоту излучения СН₄-лазера, а по криптоновому стандарту частоты - его длину волны (около 3,39 мкм) и получили с = 299792456,2 = 0,8 м/сек. К настоящему времени (1976) по решению XII Генеральной ассамблеи Международный союза по радиосвязи (1957) принято считать С. с. в вакууме равной 299792 = 0,4 км/сек.

Знание точной величины С. с. имеет большое практическое значение, в частности в связи с определением расстояний по времени прохождения радио- или световых сигналов в радиолокации, оптической локации и дальнометрии. Особенно широко этот метод применяется в геодезии и в системах слежения за искусственными спутниками Земли; он использован для точного измерения расстояния между Землёй и Луной и для решения ряда других задач.

Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии. Геометрическая оптика, оставаясь приближенным методом построения изображений в оптических системах, позволяет разобрать основные явления, связанные с прохождением через них света, и является поэтому основой теории оптических приборов.  Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая — сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п. По внешней форме (рис. 232) линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие.

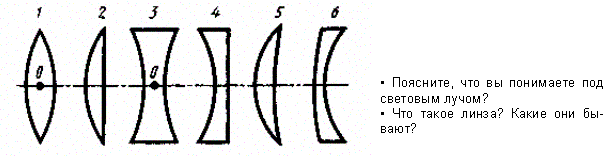Рис. 232

Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр Олинзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линз с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр Олежит на пересечении главной оптической оси со сферической поверхностью).  Для вывода формулы тонкой линзы — соотношения, связывающего радиусы кривизны R1 и R2поверхностей линзы с расстояниями а и bот линзы до предмета и его изображения, — воспользуемся принципом Ферма*, или принципом наименьшего времени: действительный путь распространения света (траектория светового луча) есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками.  Рассмотрим два световых луча (рис. 233) — луч, соединяющий точки А и В (луч ЛОВ), и луч, проходящий через край линзы (луч АСВ), — воспользовавшись условием равенства времени прохождения света вдоль АО В и АСВ. Время прохождения света вдоль АОВ 

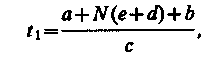
где N = n/n1— относительный показатель преломления (n и n1— соответственно абсолютные показатели преломления линзы и окружающей среды). Время прохождения света вдоль АСВ равно 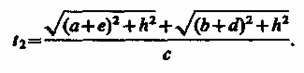 Так как t1 = t2, то                  (166.1)

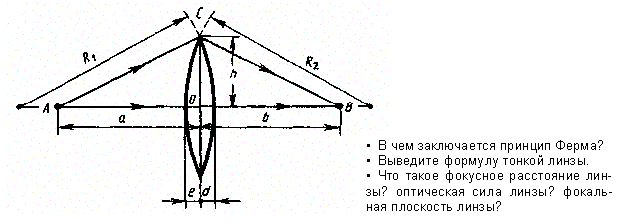Рис. 233

 Рассмотрим параксиальные (приосевые) лучи, т. е. лучи, образующие с оптической осью малые углы. Только при использовании параксиальных лучей получается стигматическое изображение, т. е. все лучи параксиального пучка, исходящего из точки А, пересекают оптическую ось в одной и той же точке В. Тогда h ≪ (a+e), h ≪ (b+d) и  Аналогично, 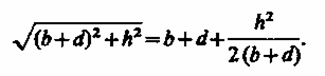 Подставив найденные выражения в (166.1), получим 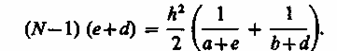                             (166.2)  Для тонкой линзы е ≪ а и d≪ b, поэтому (166.2) можно представить в виде 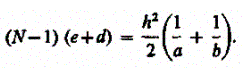 Учитывая, что  и соответственно d= h2/(2R1), получим 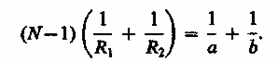                               (166.3)  Выражение (166.3) представляет собой формулу тонкой линзы. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой — отрицательным. Если a = ¥, т. е. лучи падают на линзу параллельным пучком (рис. 234, а), то 

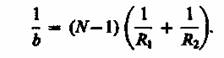
                      Рис. 234

 Соответствующее этому случаю расстояние b = OF = f называется фокусным расстоянием линзы, определяемым по формуле  Оно зависит от относительного показателя преломления и радиусов кривизны.  Если b = ¥, т. е. изображение находится в бесконечности и, следовательно, лучи выходят из линзы параллельным пучком (рис. 234, 6), то a = OF = f. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус — это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.  Величина 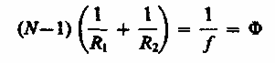                                (166.4)  называется оптической силой линзы. Ее единица — диоптрия (дптр). Диоптрия — оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр= 1/м.  Линзы с положительной оптической силой являются собирающими, с отрицательной — рассеивающими. Плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси, называются фокальными плоскостями. В отличие от собирающей рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси (рис. 235). 

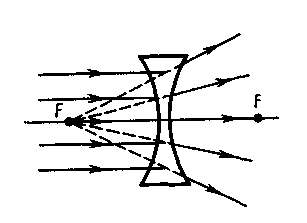
Рис. 235

Учитывая (166.4), формулу линзы (166.3) можно записать в виде 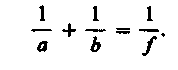  Для рассеивающей линзы расстояния/и bнадо считать отрицательными.  Построение изображения предмета в линзах осуществляется с помощью следующих лучей:

• луча, проходящего через оптический центр линзы и не изменяющего своего направления;

• луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;

• луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси.

Для примера приведены построения изображений в собирающей (рис. 236) и в рассеивающей (рис. 237) линзах: действительное (рис. 236, а) и мнимое (рис. 236, б) изображения — в собирающей линзе, мнимое — в рассеивающей. 

                                      Рис. 236

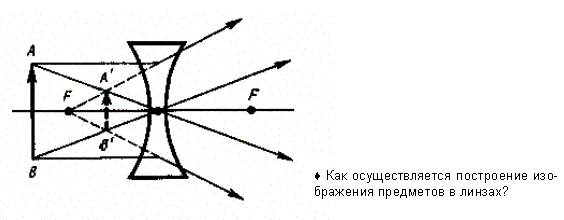Рис. 237

Отношение линейных размеров изображения и предмета называется линейным увеличением линзы. Отрицательным значениям линейного увеличения соответствует действительное изображение (оно перевернутое), положительным — мнимое изображение (оно прямое). Комбинации собирающих и рассеивающих линз применяются в оптических приборах, используемых для решения различных научных и технических задач.