Формула перехода от одного основания логарифма к другому

Переход к логарифмам с новым основанием осуществляется по правилу, которое можно выразить так: логарифм числа по старому основанию равен логарифму того же числа по новому основанию, деленному на логарифм старого основания по новому основанию:  .

28 Решение показательных уравнений и неравенств

Ответ :

Показательные уравнения и неравенства — это уравнения и неравенства, в которых переменная

величина входит в аргумент показательных функций.

29 Решение логарифмических уравнений и неравенств

Ответ :

Логарифмические уравнения и неравенства — это уравнения и неравенства, в которых

переменная величина находится под знаком логарифма

30 Соответствия между градусной и радианной мерами углов .

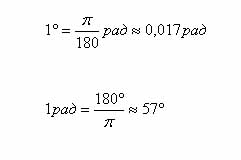
31 Тригонометрические функции числового аргумента , знаки их значений .

Ответ :

Тригонометрические функции числового аргумента

1. Угол (дуга) в тригонометрии измеряется в градусах и радианах:

а его величина положительна или отрицательна в зависимости от того, отсчитывается ли он от начального радиуса О А (точки A) против или по часовой стрелке (рис. 4).

2. Единичную окружность

u² + v² = 1

отнесем к прямоугольной системе координат Оuv. Каждой точке M(u;v) этой окружности (u -- абсцисса, v -- ордината М) соответствует бесконечное множество угловых (дуговых) координат:

3. Тригонометрические функции синус, и косинус определяются при помощи координат u и v точки М:

sin a = и, cos а = и.

Знак перед корнем выбирается в зависимости от величины .

         Суммы или разности Т. ф. различных аргументов могут быть преобразованы в произведения по следующим формулам:

         

Две другие функции -- тангенс и котангенс -- можно определить следующим образом (рис. 5). Касательную At(Bт) превратим в числовую прямую с началом в точке A(В), положительным направлением вверх (вправо) и единицей масштаба, равной радиусу окружности. Через t(т) обозначим координату точки пересечения прямой ОМ с осью тангенсов At (котангенсов Bт).

Знаки тригонометрических функций по четвертям

В таблице приведены знаки тригонометрических функций (sin, cos, tg, ctg) по четвертям в тригонометрическом круге.

ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПО ЧЕТВЕРТЯМ В ТРИГОНОМЕТРИЧЕСКОМ КРУГЕ
Функция / четверть	I	II	III	IV
sin б	+	+	-	-
cos б	+	-	-	+
tg б	+	-	+	-

32 Соотношение между тригонометрическими функциями одного аргумента

Ответ :

Соотношения между тригонометрическими функциями одного аргумента

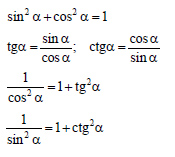
33 Формулы привидения

Ответ :

π/2 – α π/2 + α π – α π + α 3π/2 – α 3π/2 + α 2π – α 2π + α

34 Тригонометрические функции суммы и разности двух углов

Ответ :

Тригонометрические функции суммы и разности углов

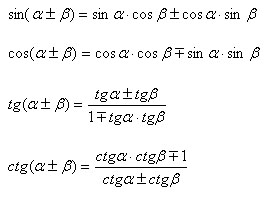
35 Тригонометрические функции двойного угла

Ответ :

sin(2α)- через sin и cos:

 

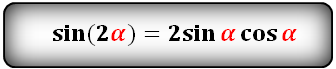
sin(2α)- через tg и ctg:

 

cos(2α)- через sin и cos:

 

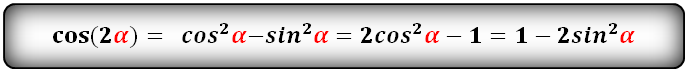
cos(2α)- через tg и ctg:

 

 

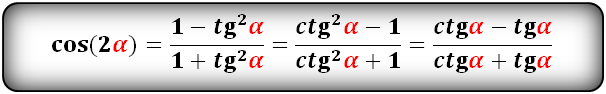
tg(2α) и сtg(2α):

 

 

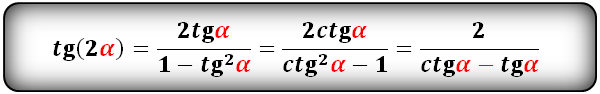
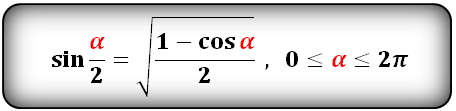
36 Тригонометрические функции половинного аргумента

Ответ :

 

 

 

 

 

37 Формулы понижения степени

Ответ :

38 Преобразование суммы и разности одноименных тригонометрических функций и произведение

Ответ :

1. Сумма синусов 

2. Разность синусов 

3. Сумма косинусов 

4. Разность косинусов 

5. Сумма тангенсов 

6. Разность тангенсов 

7. Сумма котангенсов 

8. Разность котангенсов 

9. Сумма косинуса и синуса 

10. Разность косинуса и синуса 

11. Сумма тангенса и котангенса 

12. Разность тангенса и котангенс

13

14

15

16

39 Тригонометрическая функция у =sinx, её график и свойства

Ответ :

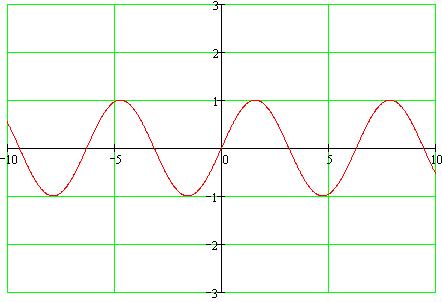
Основные свойства:

1. Область определения вся числовая ось.

2. Функция ограниченная. Множество значений – отрезок [-1;1].

3. Функция нечетная.

4.Функция периодическая с наименьшим положительным периодом равным 2*π.

40 Тригонометрическая функция у = соsx , её графики свойства

Ответ :

График функции y=cos(x).

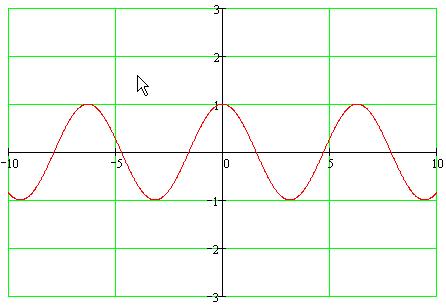
Основные свойства:

1. Область определения вся числовая ось.

2. Функция ограниченная. Множество значений – отрезок [-1;1].

3. Функция четная.

4.Функция периодическая с наименьшим положительным периодом равным 2*π.

41 Тригонометрическая функция у =tgx, её график и свойства

Ответ :

График функции y=tg(x).

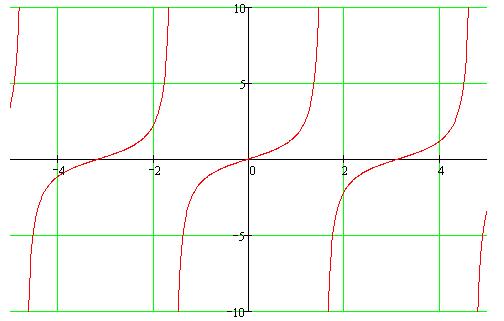
Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.

2. Функция неограниченная. Множество значение вся числовая прямая.

3. Функция нечетная.

4.Функция периодическая с наименьшим положительным периодом равным π.

42 Тригонометрическая функция у= ctgx, eё график и свойства

Ответ :

График функции y=ctg(x).

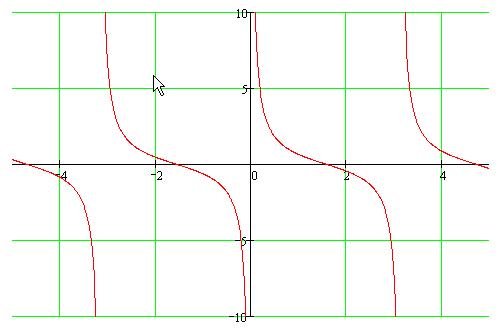
Основные свойства:

1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.

2. Функция неограниченная. Множество значение вся числовая прямая.

3. Функция нечетная.

4.Функция периодическая с наименьшим положительным периодом равным π.

43 Обратные тригонометрические функции

Ответ :

Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)

• аркко́синус (обозначение: arccos)

• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)

• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccotan)

• арксе́канс (обозначение: arcsec)

• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

44 Решение простейших тригонометрических уравнений

Ответ :

Простейшие тригонометрические уравнения — это урав-

нения следующих видов:

cos x = a; sin x = a; tg x = a; ctg x = a

45 Решение тригонометрических неравенств sinx ‹ a sinx›a

Ответ :

.

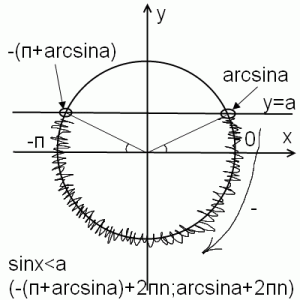
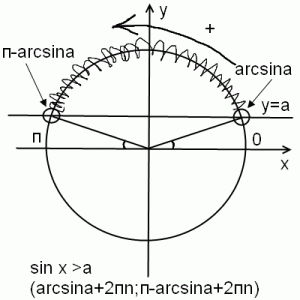
46 Решение тригонометрических неравенств cos x‹a cos x ›a

Ответ :

47 Решение тригонометрических неравенств tgx‹a tgx›a

Ответ :

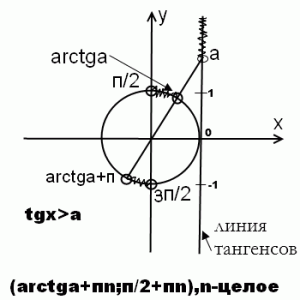
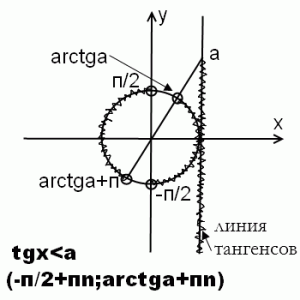
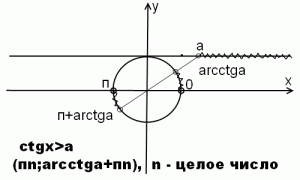
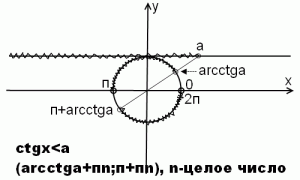
48 Решение тригонометрических неравенств сtg‹a ctg›a

Ответ :