Предел функции в бесконечности

Пусть функция f(x) определена на (a, + ∞).

Число A называется пределом функции f(x) при x → + ∞ (обозначается A = 

lim

x → + ∞

 f(x) ), если

 ε > 0     N:     x > N      |f(x) − a| < ε.

Пусть функция f(x) определена на ( − ∞,a).

Число A называется пределом функции f(x) при x → − ∞ (обозначается A = 

lim

x → − ∞

 f(x) }, если

 ε > 0     N:     x < − N      |f(x) − a| < ε.

Если существуют пределы функции f(x) при x → + ∞ и при x → − ∞ и они равны одному и тому же числу A, то это число A называется пределом функции f(x) приx → ∞ {обозначается A = 

lim

x → ∞

 f(x) .

Теоремы о пределах последовательностей и правила их вычисления распространяются и на пределы функций в бесконечности.

Наклонные асимптоты графика функции

Пусть функция f(x) определена на (a, + ∞). Обозначим символом α разность ординат точек графика функции f(x ) и прямой y = kx + b при одном и том же значении x(рис. 1), т.е. α(x) = f(x) − (kx + b).

18 Вычисление предела функции в бесконечности . Правила раскрытия неопределённостей вида бесконечность делить на бесконечность и бесконечность –бесконечность

Пусть функция f(x) определена на (a, + ∞).

Число A называется пределом функции f(x) при x → + ∞ (обозначается A = 

lim

19 Бесконечная числовая последовательность . Предел числовой последовательности .

Ответ :

Числовая последовательность — это последовательность элементов числового пространства. 

Предел числовой последовательности — предел последовательности элементовчислового пространства

20 Степенная функция с натуральным показателем .

Ответ :

Степенная функция с натуральным показателем y = xn n ∈ N непрерывна на множестве действительных чисел. Если n нечетное, то эта функция строго возрастает и потому обратима. Обратной к ней является функция.

21 Степенная функция с целым отрицательным показателем .

Ответ :

Степенная функция с целым отрицательным показателем вида (картинка) имеет график функции, изображенный на рисунке. Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой .

22 Степенная функция с показателем вида 1/n

Ответ :

степенная функция с показателем вида 1/n - это корень n-ой степени

23 Показательная функция , её графики и свойства

Ответ :

Показательная функция — математическая функция , где   называется основанием степени, а   — показателем степени.

Свойства

a^x*a^y = a^{(x + y)};

(a^x)/(a^y) = a^(x-y);

(a*b)^x = (a^x)*(a^y);

(a/b)^x = a^x/b^x;

(a^x)^y = a^{(x * y)}

На следующем рисунке представлен график возрастающей показательной функции: a>0.

На следующем рисунке представлен график убывающей показательной функции: 0<a<1.

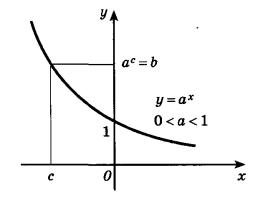
24 Логарифмическая функция , её графики и свойства

Ответ :

Функция y = loga x , а больше 0 а не = 0 называется логарифмической

Свойства логарифмической функции

1. Область определения функции D( f )  (0;).

2. Множество значений E( f )  R.

3. y x a = log – монотонная функция, причем возрастающая при a больше 1

( x x x x 1  2  a 1  a 2

log ) и убывающая при 0 a меньше 1

( x x x x 1  2  a 1  a 2

log log ).

Из монотонности логарифмической функции следует, в частности, что если для

1 2 1 2

x , x 0 log x log x  a  a

, то 1 2

x  x .

25 Логарифмы и их свойства . Десятичные и натуральные логарифмы .

Ответ :

Логарифм положительного числа   по основанию   (обозначается  ) — это показатель степени, в которую надо возвести  , чтобы получить  . b > 0, a > 0, а≠ 1.

Свойства

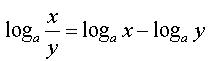
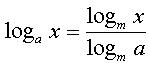
Натуральный логарифм

ln(e)=1;  ln(1)=0

При		логарифм числа (1+х) разлагается в ряд:

ln(e)=1;  ln(1)=0

При		логарифм числа (1+х) разлагается в ряд:
Десятичный логарифм lg (логарифм по основанию "10").  lg(10)=1;  lg(1)=0
Если: а = b · 10 n То: lg a = lg b + n Кроме того: 10 x = 10 { x } · 10 [ x ] , где { x } — дробная часть x , а [ x ] — целая часть x .

26 Логарифмирование и потенцирование .

Ответ :

Логарифмирование – это нахождение логарифмов заданных чисел или выражений.

Потенцирование – это нахождение чисел или выражений по данному логарифму числа (выражения).

27 Формулы перехода от одного основания логарифма к другому

Ответ :