Вопросы к экзамену по математике 1 курс , 1 семестр . И ответы.

1. Математика и научно - технический процесс. Понятие о математическом моделирование .

Ответ :

Научно-технический прогресс — это процесс непрерывной по развитию науки, техники, технологии, совершенствования предметов труда, форм и методов организации производства» и труда. 

Математическое моделирование — описание анализируемого объекта внешнего мира с помощью математической символики.

2. Десятичное приближение действительных чисел . Абсолютная и относительная погрешности их границы .

Ответ :

Десятичное действительное число - приближенное изображение действительного числа конечной десятичной дробью. Всякое   десятичное число может быть записано в виде бесконечной десятичной дроби.

 Абсолютная погрешность  – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.

Относительная погрешность – это число, отражающее степень точности измерения.

граница абсолютной, и относительной погрешностей- это максимальное и минимальное допустимое значение величины исходя из этих погрешностей.

3 Верные и Сомнительные числа . Запись приближённых чисел . Округление приближённых чисел .

Цифра m приближённого числа a называется верной в широком смысле , если граница абсолютной погрешности числа a не превосходит единицы того разряда в котором записывается цифра m

Цифры в записи приближенного числа о которых не известно , являются ли они верными , называются сомнительными .

Округление

Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры округленного числа. Поэтому, чтобы после округления все знаки были верны, погрешность до округления должна быть не больше половины единицы того разряда, до которого предполагают делать округление.

4. Правила строгого учета погрешностей при выполнении действий с приближёнными числами .

Ответ :

Существуют строгие и нестрогие методы оценки точности результатов вы-

числений. К первой группе методов относятся:

– строгий метод итоговой оценки;

– метод строгого пооперационного учета погрешностей.

Суть строгого метода итоговой оценки состоит в том, что если прибли-

женные вычисления выполняются по сравнительно простой формуле, то с по-

мощью формул учета погрешностей арифметических действий и вычисления

функции можно вывести формулу итоговой погрешности

5 Правила подсчета цифр при выполнение действий с приближёнными числами .

Ответ :

В этом правиле используются понятия десятичных знаков, значащих цифр, точных и сомнительных цифр. Напомним, что десятичными знаками числа называют все его цифры, стоящие правее запятой. 

6. Понятие комплексного числа . Действия с комплексными числами , заданные в алгебраической форме .

Ответ :

Комплексным числом-   Комплексным числом называется выражение вида a  +  ib , где a  и  b – любые действительные числа, i – специальное число, которое называется мнимой единицей . 

Действия над комплексными числами в алгебраической форме.

Суммой двух комплексных чисел a+bj и c+dj называется комплексное число (a+c)+(b+d)j. a+bj + c+dj=(a+c)+(b+d)j. Сложение комплексных чисел обладает свойствами:

1). z1+z2=z2+z1 переместительный з-н.

2). (z1+z2)+z3=z1+z2+z3 сочетательный з-н.

3). z1-z2=z3, z3+z2=z1

Разностью комплексных чисел z1 и z2 называется такое число z3, которое в сумме с z2 дает z1. Теорема: Для любых комплексных чисел z1 и z2 разность z3=z1+z2 определена и причем однозначно. Правило: (a+bj)-(c+dj)=(a-c)+(b-d)j.

Произведением комплексных чисел a+bj и c+dj называется комплексное число(ac-bd)+(ad+bc)j. (a+bj)+(c+dj)=ac+adj+bcj+bdj².

Частным от деления комплексного числа z1 на z2 (z2≠0+0j) называется такое число z3, которое при умножении на z2 дает z1. Теорема: частное двух комплексных чисел z1  и z2 (z2≠0+0j) определено и причем однозначно

6. определение функций . Понятия числовой , обратимой сложной функций.

Ответ :

Определение  функции- выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. 

Понятие обратной функции - Функция   называется обратимой, если для любых двух различных чисел   и  , принадлежащих  , числа  и   также различны.

6. График функции. Преобразование графиков функций без изменения масштаба .

Ответ :

График функции — которое даёт представление о геометрическом образе функции.

Преобразование графиков функций

Функция	Преобразование графика функции
	Параллельный перенос вдоль оси OY на A единиц вверх, если А>0, и на |A| единиц вниз, если А<0.
	Параллельный перенос вдоль оси OX на a единиц вправо, если a > 0, на |a| единиц влево, если a < 0.
	Растяжение вдоль оси OY относительно оси OX в k раз, если k > 1, и сжатие в 1/kраз, если 0 < k < 1.
	Сжатие вдоль оси OX относительно оси OY в k раз, если k > 1, и растяжение в 1/kраз, если 0 < k < 1.
	Симметричное отражение относительно оси OX
	Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси, остальная его часть остается без изменения.
	Симметричное отражение относительно оси OY.
	Часть графика, расположенная в области x  0, остается без изменения, а его часть для области x  0 заменяется симметричным отображением относительно оси OY части графика для x  0.

6. График функции . Преобразование графиков функций с изменения масштаба .

Ответ :

График функции — которое даёт представление о геометрическом образе функции.

Преобразование графиков функций

Функция	Преобразование графика функции
	Параллельный перенос вдоль оси OY на A единиц вверх, если А>0, и на |A| единиц вниз, если А<0.
	Параллельный перенос вдоль оси OX на a единиц вправо, если a > 0, на |a| единиц влево, если a < 0.
	Растяжение вдоль оси OY относительно оси OX в k раз, если k > 1, и сжатие в 1/kраз, если 0 < k < 1.
	Сжатие вдоль оси OX относительно оси OY в k раз, если k > 1, и растяжение в 1/kраз, если 0 < k < 1.
	Симметричное отражение относительно оси OX
	Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси, остальная его часть остается без изменения.
	Симметричное отражение относительно оси OY.
	Часть графика, расположенная в области x  0, остается без изменения, а его часть для области x  0 заменяется симметричным отображением относительно оси OY части графика для x  0.

6. Построение графиков функций , аналитическое выражение которых содержит знак модуля .

Ответ :  у = |х|

1. Если х 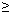  0, то |х| =х и наша функция у =х, т.е. искомый график совпадает с биссектрисой первого координатного угла.

2. Если х<0, то |х|= -х и у= -х. При отрицательных значениях аргумента х график данной функции - прямая у= -х, т.е. биссектриса второго координатного угла.

Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)

6. Свойства монотонности и ограниченности функции

Ответ :

Моното́нная фу́нкция — это функция, приращение  которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное^. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.