1.Определение 1. Угловой величиной дуги называется отношение длины этой дуги к длине окружности, умноженное на 2π.Теорема 1. Величина центрального угла равна угловой величине дуги, на которую он опирается.Теорема 2. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается. Следствие. Вписанные углы, опирающиеся на одну и ту же дугу или на равные дуги одной окружности, равны.Теорема 3. Угол между касательной и хордой, выходящими из одной точки окружности, измеряется половиной угловой величины дуги, заключенной внутри этого угла (рис. 1).
Теорема
4. Угол,
вершина которого расположена вне круга,
измеряется полуразностью угловых
величин дуг окружности этого круга,
заключенных внутри угла (рис. 2).
2.
Пусть
–
угол между подвижным радиус-вектором
OM=
{ x,
y}
и его
начальным положением OA.
а)
Синусом
угла
называется
отношение ординаты y
конца подвижного радиус-вектора
r
= OM
к
длине r
= | r |
этого
радиус-вектора, т.е.
б)
Косинусом
угла
называется
отношение абсциссы x
конца подвижного радиус-вектора r
= OM
к
длине r
= | r |
этого
радиус-вектора, т.е.
в) Тангенсом
угла
называется
отношение ординаты y
к абсциссе x
конца
подвижного радиус-вектора OM
. т.е.
г) Котангенсом
угла
называется
отношение абсциссы x
к ординате y
конца
подвижного радиус-вектора OM
, т.е.
д) Функции секанс
и косеканс
определяются
соотношениями
3.
Следует
иметь в виду, что указанные равенства
верны при всех значениях
x,
при которых их левая и
правая части одновременно имеют
смысл (т.е. в областях определения)
и их называют основными
тригонометрическими тождествами.
При
использовании тождеств
необходимо
учитывать области их определения.
Например, областью определения тождества
является
все множество действительных чисел
R;
область определения тождества
задается
условием
область
определения тождества
–
условием
4. Формулы сложения аргументов
Синус суммы двух чисел равен сумме произведений синуса первого числа на косинус второго и косинуса первого числа на синус второго:
Доказательство строится с использованием формул приведения:
,
что и требовалось доказать.
Формулы сложения функций
(в
последних двух формулах
и
соответственно
);
(в
последних двух формулах
и
соответственно
).
5.
Формулы для двойных углов |
Для любого угла α справедливы равенства:
sin 2α = 2sinα cosα |
cos 2α = cos2α – sin2α = 2 cos2α – 1 = 1 – 2sin2α |
Для любого угла α такого, что α ≠ π/2 + πk, α ≠ π/4 + πn/2 (k, n принадлежат множеству Z), справедливо:
tg 2α = 2 tgα/(1 – tg2α) |
Для любого угла α такого, что α ≠ πk/2 (k принадлежит множеству Z), справедливо:
сtg 2α = (ctg2α – 1)/(2ctgα) |
Формулы для половиннных углов |
Для любого угла α справедливы равенства:
cos2α/2 = (1 + cos α)/2 |
sin2α/2 = (1 – cos α)/2 |
Для любого угла α такого, что α ≠ π + 2πk (k принадлежит множеству Z), справедливо:
-
tg2α/2 = (1 – cos α)/(1 + cos α)
ctg2α/2 = (1 + cos α)/(1 – cos α)
tg α/2 = sin α/(1 + cos α)
cos α = (1 – tg2α/2)/(1 + tg2α/2)
sin α = (2 tg α/2)/(1 + tg2α/2)
Для любого угла α такого, что α ≠ πk (k принадлежит множеству Z), справедливо:
tg α/2 = (1 – cos α)/(sin α) |
ctg α = (1 – tg2α/2)/(2 tg α/2) |
Для любого угла α такого, что α ≠ π + 2πk и α ≠ π/2 + πn (k, n принадлежат множеству Z), справедливо:
tg α = (2 tg α/2)/(1 – tg2α/2) |
6. Формулы приведения - это сокращенное название формул, которые позволяют привести синусы и косинусы к соответствующим значениям синусов и косинусов острых углов (т.е. от 0 до 90 градусов). Кроме того, формулы приведения существуют для тангенсов и катангенсов.
Формулы приведения хорошо объясняются с помощью различных поворотов и отражений точки, соответствующей углу, на единичной окружности (смотрите в видео).
Формулами приведения для синуса являются следующие семь формул:
Формулами приведения для косинуса являются следующие семь формул:
7.
Четность тригонометрических функций. Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки). |
|
|
Поэтому конечные стороны OA1 и ОА2 этих углов симметричны относительно оси абсцисс. Координаты векторов единичной длины OA1 = (х1 , у1) и ОА2 = (х2, y2) удовлетворяют соотношениям: х2 = х1 y2 = —у1 Поэтому cos(—φ) = cosφ, sin (— φ) = —sin φ, Следовательно, синус является нечетной, а косинус — четной функцией угла. |
||
Далее имеем:
|
||
Поэтому тангенс и котангенс являются нечетными функциями угла. |
||
Периодичность функций sin φ и cos φ
|
||
Предположим, что вектор ОА = (х, у) единичной длины образует с осью абсцисс угол φ. Если сделать полный оборот вектора ОА вокруг точки О против часовой стрелки, то получится угол φ + 360°. Но вектор ОА при этом займет первоначальное положение, а потому координаты его х и у не изменятся. |
|
|
Следовательно, у = sin φ = sin(φ + 360°), x = cos φ = cos (φ+ 360°). Эти соотношения показывают, что значения функций sin φ и cos φ не изменяются, если их аргумент, увеличить на 360°. Пусть f(х) есть некоторое выражение, зависящее от переменной величины х. (Например, f(х) = x2, f(х) = sin x и т. д.) Тогда равенство y = f(х) Определяет у как функцию аргумента х. |
||
Если при любых допустимых значениях аргумента х f(x+T) = f (х), где Т — некоторое отличное от нуля число, то функция f (x) называется периодической, а число Т — ее периодом. Согласно этому определению функции sin x и cos х являются периодическими с периодом Т = 360°. При n полных оборотах вектора ОА против часовой стрелки образуется угол φ + 360°n, а по часовой стрелке — угол φ — 360°n. В каждом из этих случаев координаты х и у вектора не изменяются, а потому не изменяются sin φ и cos φ. Таким образом, cos φ = cos (φ + 360°n), sin φ = sin (φ + 360°n), (1) где n — любое целое число (положительное, отрицательное или нуль). Формулы (1) показывают, что каждый из углов 360°; 720°; 1080°; ... (n = 1, 2, 3, . . .), — 360°; —720°; —1080°; ... (n = — 1, —2, —3, . . .) является периодом функции sin φ и cos φ. Таким образом, эти периодические функции имеют бесконечное множество периодов. |
||
8. Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
аркси́нус (обозначение: arcsin)
аркко́синус (обозначение: arccos)
аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
арксе́канс (обозначение: arcsec)
арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.
Основное соотношение
Функция arcsin
График
функции
.
Арксинусом
числа m
называется такое значение угла x,
для которого
Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция
является
строго возрастающей.
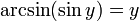при
при
(область
определения),
(область
значений).
9.
Определение:
Арксинусом
числа а
называется угол из отрезка
,
синус которого равен числу а.
Свойство арксинуса от отрицательного угла :
Определение:
Аркосинусом
числа а
называется угол из отрезка
,
косинус которого равен числу а.
Свойство арккосинуса от отрицательного угла :
Определение:
Арктангенсом
числа а
называется угол из интервала
,
тангенс которого равен числу а.
Свойство арктангенса от отрицательного угла :
Определение:
Арккотангенсом
числа а
называется угол из интервала
,
котангенс которого равен числу а.
Свойство арккотангенса от отрицательного угла :
10. Ключевые слова: тригонометрия, синус, косинус, тангенс, котангенс, cos, sin, tg, ctg, тригонометрические уравнения, частные формулы тригонометрических уравнений
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Уравнения
вида sin
x = a;
cos x = a;
tg x = a;
ctg x = a,
где x
- переменная, a
R,
называются простейшими
тригонометрическими уравнениями.
11.
Пусть
и
Тогда
существует единственное неотрицательное
число x такое, что выполняется равенство
Это
число называется арифметическим корнем
n -ной степени из неотрицательного числа
и обозначается
При
этом число a называется подкоренным
числом , а число n − показателем корня
.
Вместо
слова «корень» часто говорят радикал
. Если n = 2, то обычно пишут просто:
При
n = 2 арифметический корень называется
квадратным корнем , при n = 3 говорят
о кубическом корне .
Итак,
по определению:
Отсюда
следует, что
Например,
се свойства формулируются и доказываются только для неотрицательных значений переменных, содержащихся под знаками корней.
Доказательство.
Введем
следующие обозначения:
Нам надо доказать, что для неотрицательных
чисел х, у, z выполняется равенство
х-уz.
Так как
Итак,
Но
если степени двух неотрицательных чисел
равны и показатели степеней равны, то
равны и основания степеней;
значит, из равенства xn
=(уz)п
следует, что х-уz, а это и требовалось
доказать.
12.
Определение.
Степенью числа a>0 с рациональным
показателем 
,
где m
- целое число, а n
- натуральное ( n>1), называется число
,
т.е.
Свойства степени с рациональным показателем.
