39. Смешанное произведение векторов. Свойства. Доказательство одного свойства. Смешанное произведение векторов

Смешанным произведением векторов называется число, равное скалярному произведению векторного произведения на

Свойства смешанного произведения

1. Необходимое и достаточное условие компланарности векторов - смешанное произведение векторов равно 0:

Доказательство.

Необходимость. Если векторы компланарны, то вектор перпендикулярен плоскости векторов и, следовательно, и вектору а тогда

Достаточность. Пусть тогда по определению скалярного произведения

Здесь угол между векторами и Поэтому

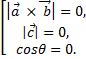
Тогда либо 1) , следовательно, компланарны; либо 2) , следовательно, компланарны; либо то есть вектор перпендикулярен вектору , следовательно, компланарны.

2. Смешанное произведение некомпланарных векторов по модулю равно объему параллелепипеда , построенного на векторах сомножителях, приведенных к общему началу. Смешанное произведение положительно, если векторы образуют правую тройку, смешанное произведение отрицательно, если векторы образуют левую тройку.

Доказательство.

Пусть - площадь параллелограмма, построенного на векторах приведенных к общему началу, вектор - орт вектора высота параллелепипеда, построенного на векторах приведенных к общему началу. Понятно, что

Если векторы образуют правую тройку (рис. 4), то если векторы образуют левую тройку (рис.5), то

Поэтому

Рис.4 Рис. 5

3. 

Доказательство. Действительно, все смешанные произведения по модулю равны объему одного и того же параллелепипеда. Первые 3 тройки и последние 3 тройки векторов – одной ориентации.

Если все векторы компланарны, то все смешанные произведения равны 0.

Следствие.

Равенство перепишем в виде

4. Смешанное произведение обладает свойством линейности относительно любого сомножителя.

Доказательство. В силу линейности скалярного произведения относительно первого сомножителя

Применяя свойство 3, получаем свойство линейности смешанного произведения относительно второго и третьего множителей

5. Если известны координаты векторов то

Доказательство. Разложим определитель по элементам третьей строки

41. Алгебраические линии первого порядка. Различные виды уравнений прямой на плоскости. Определение расстояния от точки до прямой. Прямая на плоскости

Теорема. Алгебраические линии первого порядка – прямые.

Доказательство.

1. Покажем, что уравнение любой прямой на плоскости – алгебраическое уравнение 1 порядка. Пусть на плоскости задана прямая Выберем декартову прямоугольную систему координат так, чтобы ось совпала с прямой Тогда уравнение прямой в этой системе координат , так как координаты любой точки прямой удовлетворяют этому уравнению, а для любой точки, не лежащей на 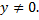Уравнение является алгебраическим уравнением первой степени, Следовательно, прямая – алгебраическая линия первого порядка.

2. Пусть дано уравнение 1-й степени

- заданные числа.

Покажем, что это уравнение определяет на плоскости прямую. Выберем точку координаты которой удовлетворяют уравнению

Тогда и уравнение можно записать в виде

или

Рассмотрим вектор и прямую, проходящую через точку перпендикулярно вектору Пусть точка лежит на прямой. Тогда вектор перпендикулярен вектору или

Легко убедиться, что если точка не лежит на прямой, то ее координаты не удовлетворяют уравнению Следовательно, уравнение и равносильное ему уравнение - уравнения прямой, проходящей через точку перпендикулярно вектору

Уравнение - заданные числа, называется общим уравнением прямой. Вектор называется вектором нормали прямой.

Общее уравнение прямой, проходящей через точку

Если для точек и ввести в рассмотрение радиус-векторы , то общее уравнение (3) может быть записано в векторной форме

Если в общем уравнении прямой все коэффициенты не равны 0, то общее уравнение называется полным. Полное уравнение можно преобразовать следующим образом

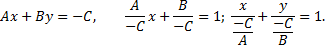
Обозначим Тогда уравнение

называется уравнением прямой в отрезках. Числа указывают, какие отрезки прямая отсекает от осей координат.